DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
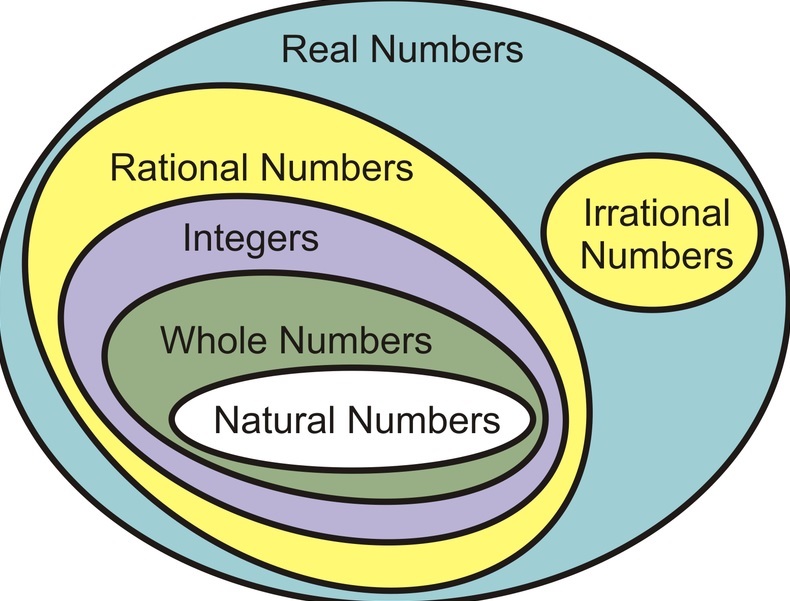
Table of Contents
REAL NUMBERS CBSE CLASS 10
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
1.If a and b are two positive integers such that a = bq + r Where q and r are unique integers. If a < b then find the value of q.
∵ a is smaller than b
∴ a = b × 0 +a
Comparing with a = bq + r we get q = 0
2.Write whether every positive integer can be of the form 4q + 2 where q is an integer. Justify your answer.
No, by Euclid’s division lemma, b = aq + r, ≤ r < a
Here b is any positive integer
a = 4
b = 4q + r for 0 ≤ r < 4
So, this must be in the from 4q, 4q + 1, 4q + 2 or 4q + 3.
3.For any positive integer n, prove that n3 – n is divisible by 6.
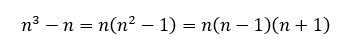
(n-1),n,(n+1) are three consecutive positive integers. One number must be divisible by 3 and one must be even number so it must be divisible by 2 and the product of these numbers must have factor product of 2 and 3 i.e., 2 × 3 = 6.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
Using Euclid’s division algorithm find the HCF (Q.4 to Q.5)
4.48250, 38540
5.273070 and 434330
Solution: 48250 = 38540 × 1 + 9710
38540 = 9710 × 3 + 9410
9710 = 9410 × 1 + 300
9410 = 300 × 31 + 110
300 = 110 × 2 + 80
110 = 80 × 1 + 30
80 = 30 × 2 + 20
30 = 20 × 1 + 10
20 = 10 × 2 + 0
∴ HCF = 10
Solution: 434330 = 273070 × 1 + 161260
273070 = 161260 × 1 + 11810
161260 = 111810 × 1 + 49450
111810 = 49450 × 2 + 12910
49450 = 12910 × 3 + 10720
12910 = 10720 × 1 + 2190
10720 = 2190 × 4 + 1960
2190 = 1960 × 1 + 230
1960 = 230 × 8 + 120
230 = 120 × 1 + 110
120 = 110 × 1 + 10
110 = 10 × 11 + 0
HCF = 10
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
6.Express the HCF of 234 and 111 as 234x + 111y , where x and y are integers.
Using Euclid’s division lemma for 234 and 111, we get
234 = 111 × 2 + 12
Now 111 = 12 × 9 + 3 and 12 = 3 × 4 + 0
∴ HCF = 3
A.T.Q. 3 = 234x + 11y
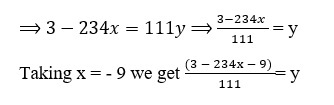
(There are no unique values of x and y.)
7.By using Euclids algorithm, find the largest number which divides 650 and 1170.
The largest number which divides 650 and 1170 = HCF of 650 and 1170 By Euclid’s division algorithm,
1170 = 650 × 1 + 520
650 = 520 × 1 + 130
520 = 130 × 4 + 0
So, HCF = 130
Hence, the largest number which divides 650 and 1170 is 130.
8.For any integer a and 3, there exists unique integers q and r such that a = 3q + r Find the possible values of r.
According to Euclids division lemma for two positive number a and b; there exists integer q and r such that a = b × q + r where 0 ≤ r < b
Here b = 3
∴ 0 ≤ r < 3
So values of r are ; 0, 1 or 2
9.Find HCF of 1001 and 385.
1001 = 385 × 2 + 231
385 = 231 × 1 + 154
231 = 154 × 1 + 77
154 = 77 × 2 + 0
∴ HCF = 77
10.When k is divided by 21; remainder = 9. Find remainder when the same number is divided by 7.
∴ k = 21q + 9, where q is some integer
⟹ k = 21q + 7 + 2
k = 7(3q + 1) + 2 = Multiple of 7 + 2
∴ k when divided by 7 will given a remainder 2.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
11. Prove that the square of any positive integer of the form 5m + 1 will leave a remainder 1 when divided by 5 for some integer m.
Let N = 5m + 1
, where
q is some integer
∴ = Multiple of 5 + 1
⟹ It will leave a remainder 1 when divided by 5.
12. N is a square of odd positive integer. Find the remainder when 5N + 3 is divided by 20.
N is square of odd positive integer
∴ N = 8q + 1, q is some integer
Now 5N = 5(8q + 1)
5N + 3 = 40q + 5 + 3
Multiple of 20 + 8
∴ 5N + 3 when divided by 20 will leave a remainder 8.
13.For some integers p and 5, there exist unique integers q and r such that p = 5q + r Possible values of r are
(a) 0 or 1
(b) 0,1 or 2
(c) 0, 1, 2 or 3
(d) 0, 1, 2, 3 or 4
Answer: (d) According to Euclids division lemma,
5 = 5q + r, where 0 ≤ r < 5
⟹ r = 0, 1, 2, 3, 4
So, possible values of r are 0, 1, 2, 3 or 4.
14. If the HCF of 55 and 99 is expressible in the form 55m – 99 , then the value of m is ____________.
55 = 5 × 11, 99 = 9 × 11
∴ HCF (55, 99) = 11
ATQ, 55 m – 99 = 11
55 × 2 – 99 = 11
m = 2
15.Find the HCF and LCM 6, 72 and 120 using fundamental theorem of arithmetic.
6= 2 × 3
72 = 2 × 2 × 2 × 3 × 3
120 = 2 × 2 × 2 × 3 × 5
Common factors of 6, 72 and 120 are 2 and 3.
HCF = 2 × 3 = 6
LCM = 2 × 2 × 3 × 3 × 5
∴ LCM = 360
16. Can we have any n ∈ N where 4n ends with the digit zero?
For unit’s digit to be 0, then should have 2 and 5 as its prime factors, but = = It does not contain 5 as one of its prime factors.
will not end with digit 0 for n ϵ N
17. The LCM of two numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then find the other number.
Let HCF = x
∴ LCM = 14x
A.T.Q. x + 14x = 600 x = 40
Now 280 × other number = HCF × LCM = 40 × 560
Other number = 80
18. Find the largest number that divides 2053 and 967 and leaves a remainder of 5 and 7 respectively.
Required number is HCF of 2053-5 and 967 – 7 = HCF of 2048 and 960 = 64
19. Can two numbers have 18 as their HCF and 380 as their LCM? Give reason.
No, because HCF is always a factor of LCM. But 18 is not a factor of 380.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
20. Find the HCF of 65 and 117 and find a pair of integral values of m and n such that HCF = 65m + 117n
Using Euclid’s division algorithm,
117 = 65 × 1 + 52
65 = 52 × 1 + 13
52 = 13 × 4 + 0
So, HCF of 117 and 65 = 13
HCF = 65m + 117n Form = 2 and n = – 1, HCF
Hence, the integral values of m and n are 2 and – 1 respectively.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
21. Show that 21n cannot end with the digits 0, 2, 4, 6 and 8 for any natural number n.
Prime factorisation of Prime factorisation of contains only prime numbers 3 and 7.
may end with the digit 0, 2, 4, 6 or 8 for some natural number n if its prime factorisation contains 2 and 5, but these are not present.
So, there is no natural number ‘n’ for which degrees ends with the digits 0, 2, 4 6 and 8.
22.If HCF of 144 and 180 is expressed in the form 13m – 3 , find the value of m.
On applying Euclid’s division algorithm,
180 = 144 × 1 + 36
144 = 36 × 4 + 0
∴ HCF of 144 and 180 is 36.
HCF = 36 = 13 × 3 – 3 which is of the form 13m – 3
Hence, m = 3
23.Determine the values of p and q so that the prime factorisation of 2520 is expressible as
Prime factorisation of 2520 is given by 2520 = × 5 × 7
It is given that
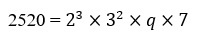
On comparing both the factorisations, we get
p = 2 and q = 5
24.The HCF of two numbers is 145 and their LCM is 2175. If one number is 725, then find the other number.
HCF × LCM = Product of two numbers
⟹ other number
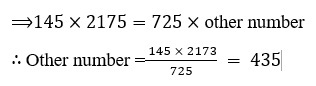
25.The HCF and LCM of two numbers are 9 and 360 respectively. If one number is 45, write the other number.
Let another number = x
HCF(45, x) = 9
LCM (45, x) = 360
HCF × LCM = 45 × x
9 × 360 = 45 × x
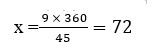
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
26.The HCF of 45 and 105 is 15. Write their LCM.
HCF (45, 105) = 15
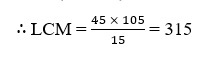
27.Find the least number which when divided by 16, leaves a remainder 6, when divided by 19 leaves a remainder 9 and when divided by 21 leaves a remainder 11.
Here, 16 – 6 = 10, 19 – 9 = 10 and 21 – 11 = 10
∴ Required number is 10 less than the least common multiple of 16, 19 and 21
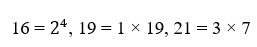
LCM = 16 × 19 × 21 = 6384
28.Find pairs of natural numbers whose least common multiple is 78 and the greatest divisor is 13.
Let numbers are 13x and 13y where x and y are coprime
∴ LCM = 13 × x × y = 78
X × y = 6
∴ Possible values of x and y
x = 1, y = 6, x = 2, y = 3
∴ Pairs of natural numbers are 78 and 13 or 26 and 39.
29.Two equilateral triangles have the sides of length: 34 cm and 85 cm respectively. Find the greatest length of tape that can measure the sides of both a them exactly.
Length of tape = HCF of 34 and 85
34 = 2 × 17
85 = 5 × 15
∴ HCF = 17
Hence length is 17.
30.P is a prime and Q is a positive integer such that P + Q = 1696. If P and Q are co-prime and their LCM is 21879, then find P and Q.
Here LCM of P and Q = 21879
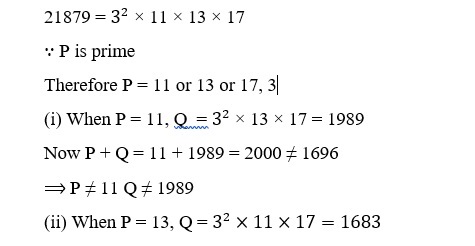
P + Q = 13 + 1683 = 1696
∴ P = 13 and Q = 1683
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
31.If x is an even number, then what is the LCM of 4x, 2x2 and x3.
x is even number
∴ x = 2q where q is some integer
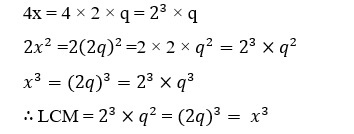
32.Find the HCF and LCM of 288, 360 and 384 by prime factorization method.
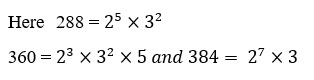
The HCF of 288, 360 and 384 is the product of their common prime factor with least exponents.
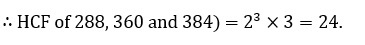
The LCM of 288, 360 and 384 is the product of all prime factor with their highest exponents.
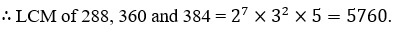
33.Let d be the HCF of 24 and 36. Find two numbers a and b, such that d = 24a + 36b.
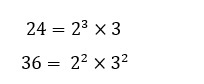
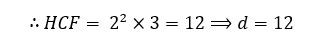
Now d = 24a + 36b
12 = 24a + 36b
When a = 5 and b = – 3 we get
12 = 24 × 5 + 36 × – 3 = 120 – 108
12 = 12
So, a = 5 , b = – 3 satisfy the eqn d = 24a + 36b
∴ one possible value of a and b is 5 and -3.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
34.There is a circular path around a sports field. Kamal takes 32 minutes to drive one round of the field while Indu takes 24 minutes for the same. Suppose they both start at the same point, and go in the same direction. After how many minutes they meet again at the starting point?
The required time is the LCM of 32 and 24.

Hence Kamal and Indu will meet again at the starting point after 96 minutes.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
35.The length, breadth and height of a room are 8 m 25 cm, 6 m 75 cm and 4 m 50 cm respectively. Determine the length of the longest rod which can measure the three dimensions of the room exactly.
Length of the longest rod = HCF of 825 cm, 675 cm and 450 cm.
825 = 3 × 5 × 5 ×11
675 = 3 × 3 × 3 × 5 × 5
450 = 2 × 3 × 3 × 5 × 5
⟹ HCF = 75
∴ Length of the longest rod = 75 cm
36. On a morning walk three persons step off together and their steps measure 40 cm, 42 cm, 45 cm, what is the minimum distance each should walk so that each can cover the same distance in complete steps?
Minimum distance = LCM of 40,42 and 45
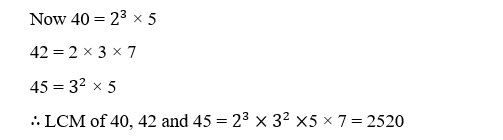
∴ They should walk 2520 cm or 25.20 m to cover the distance in complete steps.
37. P is LCM of 2, 4, 6, 8, 10 ; Q is LCM of 1, 3, 5, 7, 9 and L is LCM of P and Q. Evaluate L – 21P.
LCM of 2, 4, 6, 8, 10 = 8 × 3 × 5 = 120
⟹ P = 120
LCM of 1, 3, 5, 7, 9 = 9 × 5 × 7 = 315
⟹ Q = 315
LCM of P and Q i.e. 120 and 315
∴ L = 2520
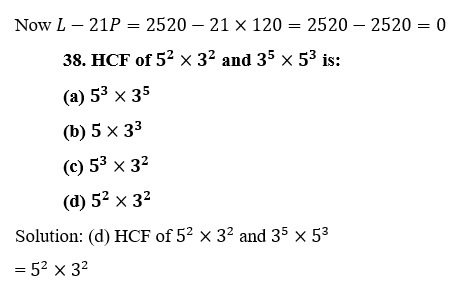
39. 4 Bells toll together at 9.00 am. They toll after 7, 8, 11 and 12 seconds respectively. How many times will they toll together again in the next 3 hours?
(a) 3
(b) 4
(c) 5
(d) 6
Solution: (c) LCM of 7, 8, 11, 12 = 1848
∴ Bells will toll together after every 1848 sec.
∴ In next 3 hrs, number of times the bells will toll together
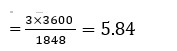
⟹ 5 times.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
40. Given that LCM (91, 26) = 182 , then HCF (91, 26) is __________.
LCM (91, 26) × HCF (91, 26) = 91 × 26
182 × HCF (91, 26) = 91 × 26



DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
ALSO VISIT:
10TH CBSE
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: REAL NUMBERS CBSE CLASS 10
