1.
If A and B are arbitrary events, then
2.
A coin is tossed three times, consider the following events
A: no head appears
B: exactly one head appears
C: atleast two heads appear Then,
4.
Two numbers x and y are chosen from 0, 1, 2, …………., 10 with replacement. The probability that | x - y | ≤ 5 is
6.
The probability that in a random arrangement of the letters of the word " FAVOURABLE” the two 'A' do not come together is
7.
The probability that a leap year will have 53 Fridays or 53 Saturdays, is
8.
If M and N are any two events, the probability that atleast one of the them occurs is K. Here, K refers to
9.
Fifteen coupons are numbered 1 to 15. Seven coupons are selected at random, one at a time with replacement. The probability that the largest number appearing on a selected coupon be 9, is
10.
Given two events A and B. If odds against A are as 2 : 1 and those in favour of A ∪ B are as 3 : 1 , then
11.
A committee of two person is selected from two men and two women. The probabilities that the committee will have (i) no man (ii) one man (iii) two men are respectively
12.
For given data which of the following option is true.
(i) P(A) = 0.5, P(B) = 0.7, P(A ⋂ B) = 0.6
(ii) P(A) = 0.5, P(B) = 0.4, P(A ∪ B) = 0.8
13.
A single letter is selected at random from the word “FAVOURABLE”. The probability that it is a vowel is
14.
A and B throw a die each. The probability, that A’s throw is not greater than B’s throw, is
15.
In a college, 25% of the boys and 10% of girls offer Mathematics. The girls constitute 60% of the total number of students. If a students is selected at random and is found to be studying Mathematics. The probability that the student is a girl is
16.
Find the probability that the birth days of six different persons will fall in exactly two calender months.
17.
A man alternately tosses a fair coin and throws a fair die beginning with the coin. The probability, that he gets a head in the coin before he gets 5 or 6 in the die, is
18.
Two cards are drawn from a pack of 52 cards. The probability that one card is an ace and other is queen, is
20.
From the employees of a company, 5 persons are selected to represent them in managing committee of the company. Particulars of five person are as follows
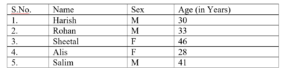
A person is selected at random from this group to act as a spokes person. What is the probability that the spokes person will be either male or over 35 year?
21.
If A and B are any two events, then P(¯A∩B) is equal to
22.
A card is drawn from a pack of playing cards. What is the probability that it will be either a king of diamond or a queen of heart.
24.
Five dice are tossed. What is the probability that the five numbers shown be different ?
25.
If A and B are any two events associated with random experiment, then by the definition of probability, which of following is true?
26.
Three ships A, B and C sail from England to India. If the ratio of their arriving safely are 2 : 5, 3 : 7 and 6 : 11, respectively, then the probability of all the ships for arriving safely is
27.
A complete cycle of a traffic light takes 60 seconds. During each cycle the light is green for 25 seconds, yellow for 5 seconds and red for 30 seconds. At a randomly chosen time, the probability that the light will not be green is
30.
Three dice are thrown together. Find the probability of getting a total of at least 6.
31.
Among 15 players, 8 are batsmen and 7 are bowlers. The probability that the team is chosen of 6 batsmen and 5 bowlers, is
32.
Consider the event A = {2,4,6,8} associated with the experiment of drawing a card from a deck of ten cards numbered from 1 to 10. Clearly, the sample space is S = {1,2 3,...10}. Then, which of the following is true?
33.
A die is thrown. Let A be the event that the number obtained is greater than 3 and B be the event that the number obtained is less than 5. Then, P(A ∪B) is
34.
If birth to a male child and birth to a female child are equal probable, then what is the probability that atleast one of the three children born to a couple is male?
35.
An urn contains n white balls numbered 1 to n, n black balls numbered 1 to n and n red balls numbered 1 to n. If two balls are drawn without replacement, then the probability, that they are of the same colour or bear the same number, is
38.
The probability distribution of a random variable X is given as
39.
A coin is tossed twice. If the second throw result in a tail, a die is thrown. Then, the total number of the outcomes of this experiment
40.
If any four numbers are selected and they are multiplied, then the probability that the last digit will be 1, 3, 5 or 7, is
42.
A basket contains 5 apples and 7 oranges and another basket contains 4 apples and 8 oranges. One fruit is picked out from each basket. The probability that the fruits are both apples or both oranges, is
44.
If a coin be tossed n times, then probability that the head comes odd times is
45.
An experiment has four possible outcomes A, B, C and D, that are mutually exclusive. Then, which of the following assignments of probabilities are permissible.
(i) P(A)=0.12, P(B) = 0.63, P(C) = 0.45 P(D) = - 0.20
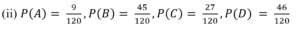
48.
A card is drawn from an ordinary pack of 52 cards and a gambler bets that, it is a spade or an ace. What are the odds against his winning this bet?
50.
The accompanying Venn diagram shows three events, A, B and C and also the probabilities of the various intersections [for instance, P(A ⋂ B) = .07]. Find P(B ⋂ C) and probability of exactly one of the three occurs.


