2.
The electric and the magnetic field, associated with an e.m. wave, propagating along the +z-axis, can be represented by: –
3.
In an electromagnetic wave,
E=1.2sin(2×106t–kx) N/C
Find value of intensity of magnetic field.
Deselect Answer
4.
In an electromagneticwave in free space the root mean square value of the electric field is Erms=6 V/m. The peak value of the magnetic field is –
Deselect Answer
5.
An em wave is propagating in a medium with a velocity .The instantaneous oscillating electric field of this em wave is along +y axis. Then the direction of oscillating magnetic field of the em wave will be along:
6.
A thin circular ring of mass M and radius 'r' is rotating about its axis with a constant angular velocity co. Four objects each of mass m, are kept gently to the opposite ends of two perpendicular diameters of the ring. The angular velocity of the ring will be: –
7.
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
8.
If a street light of mass M is suspended from the end of uniform rod of length L in the different possible patterns as shown in figure, then: –
9.
A uniform rod AB of length & and mass m is free to rotate about A. The rod is released from rest in the horizontal position. Given that the moment of inertia of the rod about A is ml2/3 the initial angular acceleration of the rod will be: –

Deselect Answer
10.
A thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity w. If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring, the ring will then rotate with an angular velocity: –
11.
A circular platform is mounted on a frictionless vertical axle, its radius R = 2m and its moment of inertia about the axle is 200 kg m². It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 ms-1 relative to the ground. Time taken by the man to complete one revolution is: –
Deselect Answer
13.
A solid sphere of mass m and radius R is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation (Esphere/Ecylinder) will be: –
Deselect Answer
14.
From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc about a perpendicular axis, passing through the centre?
Deselect Answer
15.
Two rotating bodies A and B of masses m and 2 m with moments of inertia IA and IB (IB > IA) have equal kinetic energy of rotation. If LA and LB their angular momenta respectively, then:
Deselect Answer
16.
A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 revolutions s-2 is:
Deselect Answer
17.
Find moment of inertia of a uniform annular disc of mass 100 g, having inner radius 10 cm and outer radius 20 cm, about an axis passing through its centre and perpendicular to its plane.
18.
A solid cylinder of mass 2 kg and radius 4 cm rotating about its axis at the rate of 3 rpm. The torque required to stop after 2pi revolutions is
19.
Three objects, A: (a solid sphere), B: (a thin circular disk) and C: (a circular ring), each have the same mass M and radius R. They all spin with the same angular speed about their own symmetry axes. The amounts of work (W) required to bring them to rest, would satisfy the relation.
26.
Which amongst the following compounds will show geometrical isomerism?
27.
The total number of π-bond electrons in the following structure is:
28.
Geometrical isomers differ in
29.
Consider the following reaction and identify the product (P)
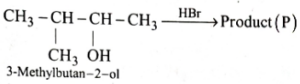
Deselect Answer
30.
Which amongst the following will be most readily dehydrated under acidic conditions?
31.
Given below are two statements:
Statement I: The acidic strength of monosubstituted nitrophenol is higher than phenol because of electron withdrawing nitro group.
Statement II: o-nitrophenol, m-nitrophenol and p-nitrophenol will have same acidic strength as they have one nitro group attached to the phenolic ring.
In the light of the above statements, choose the most appropriate answer from the options given below:
Deselect Answer
32.
What is the IUPAC name of the organic compound formed in the following chemical reaction?
33.
The structure of intermediate A in the following reaction is:
35.
Which one is the most acidic compound?
36.
The brown ring complex compound is formulated as [Fe(HO)5 NO ]SO4 The oxidation state of iron is
Deselect Answer
37.
Oxidation number of Cr in CrO5 is
38.
In which of the following compounds, the oxidation number of iodine is fractional?
39.
Oxidation amount of sodium in sodium amalgam is
40.
The process in which oxidation number increases is
41.
The oxidation number of phosphorus vary from
42.
Oxidation number of oxygen atom in O3 molecule is.
43.
In a reaction between zinc and iodine, zinc iodide is formed. Which is being oxidised?
44.
Phosphorus has the oxidation state +3 in
45.
White P reacts with caustic soda, the products are PH3 and NaH2 PO2 the reaction is an example of
Deselect Answer
51.
Let A = {1, 2, 3, 4, 5, 6, 7} Then, the relation R = {(x, y) A × A : x + y = 7} is
Deselect Answer
52.
Let R be a relation on R, given by R= {(a,b) : 3a – 3b + is an irrational number}. Then, R is
Deselect Answer
53.
Let N be the set of natural numbers and a relation R on N be defined by R = {(x, y) N × N : x3 – 3x2y – xy2 + 3y3 = 0} Then, the relation R is
Deselect Answer
54.
The domain of the function
55.
If the domain of the function
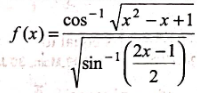
is the interval (α,β], then α+β is equal to
Deselect Answer
57.
Let A = [aij]2×2, where aij 0 for all I, j and A2 = I. Let a be the sum of all diagonal elements of A and b = |A|. Then, 3a2 + 4b2 is equal to
Deselect Answer
58.
The number of square matrices of order 5 with entries from the set {0, 1}, such that the sum of all the elements in each row is 1 and the sum of all the elements in each column is also 1, is
60.
Let P be a square matrix such that P2 = I – P. For α, β, N. If Pα + Pβ = and Pα – Pβ = ,then α + β+ – is equal to
Deselect Answer
61.
Let A and B be two square matrices of order 2. If det (a) = 2, det (B) = 3 and det((det(5(detA)B))A2) = 2a3b5c for some a, b, c N, then a+ b+ c is equal to
Deselect Answer
62.
Let A and B be two 3 × 3 real matrices such that (A2 – B2) is invertible matrix. If A5 = b5 and A3B2 = A2B3, then the value of the determinant of the matrix A3 + B3 is equal to
Deselect Answer
66.
Let P = [aij] be a 3 × 3 matrix and let Q = [bij], where bij = 2i+j aij for 1≤i, j≤3. If the determinant of P is 2, then the determinant of the matrix Q is
Deselect Answer
68.
Let the determinant of a square matrix A of order m be m-n, where m and n satisfy 4m+n=22 and 17m+4n=93. If det (n adj(adj(mA))) =3a 5b 6c , then a+ b+ c is equal to
Deselect Answer
70.
If P is a 3×3 real matrix such that PT= aP + (a-1)I, where a>1, then
Deselect Answer