DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
Table of Contents
EQUATION OF LINE CLASS 10 ICSE NOTES
1. Find the slope of a line joining following two points.
(i) A(1, 2) and B(3, – 4)
(ii) P(3, – 2) and Q(7, – 2)
(iii) X(5, 4) and Y(3, – 2)Sol. We know that, slope of a line joining two points

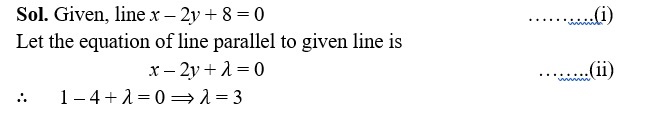
Thus, the required equation of line is x – 2y + 3 = 0.
3. The equation of a line is y = 3x – 5. Write down the slope of this line and the intercept made by its on the Y-axis. Hence or otherwise, write down the equation of a line, which is parallel to the line and which passes through the point(0, 5)
Sol. Given, line y = 3x – 5 ……….(i)
For y-intercept, put x = 0 in Eq. (i), we get
y = – 5
The slope of the line parallel to the given line will be 3 ad passes through the point
(0, 5).
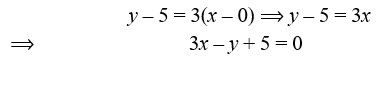
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
4. In the given figure
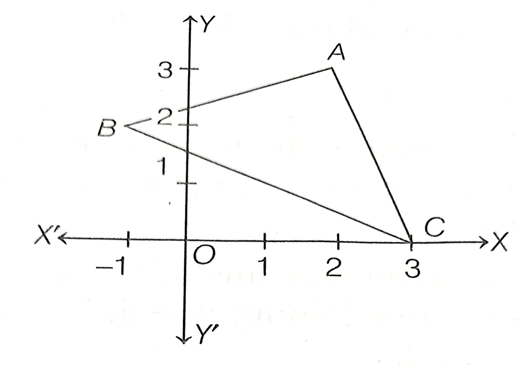
Find
(i) the coordinates of A, B and C.
(ii) the equation of a line passing through A and perpendicular to BC.

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
5. Find the value of p, for which the lines 2x + 3y – 7 = 0 and 4y – px – 12 = 0 are perpendicular to each other
Sol. Given, lines are 2x + 3y – 7 = 0 and 4y – px – 12 = 0
3y = – 2x + 7 and 4y = px + 12
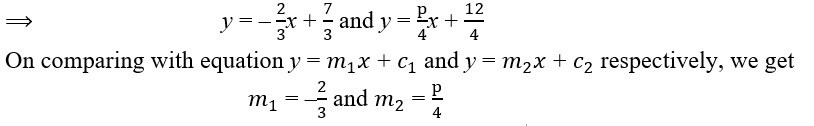
Since, the given lines are perpendicular to each other.
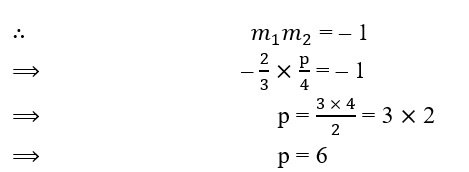
Hence, the required value of p is 6.

7. The line passing through A (– 2, 3) and B (4, b) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Sol. Given, points are A (– 2, 3) and B(4, b).
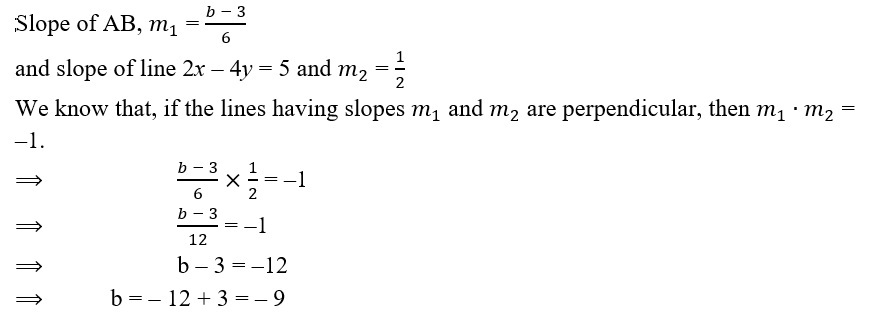
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
8. The points P(2, 3), Q(0, – 5) and R( – 2, k) are collinear, then find the value of k.
Sol. Given, P(2, 3), Q(0, – 5) and R(–2, k) are collinear points
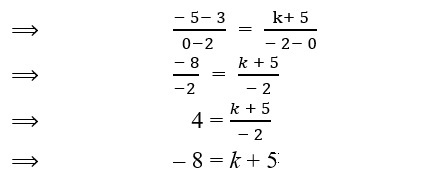
Hence, the required value of k is – 13.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
9. (i) Write down the coordinates of the point P, that divides the line joining A (– 4, 1) and B(17, 10) in the ratio 1 : 2.
(ii) Calculate the distance OP, where O is origin.
(iii) Find the equation of a line AB.
Sol. (i) Given, points are A(– 4, 1) and B(17, 10) and ratio = 1 : 2
Let the coordinates of P be(x, y).

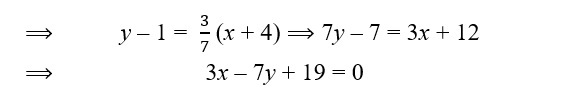
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
10. If A(1, 4), B(3, 2) and C(7, 5) are the vertices of a angle ABC. Find the coordinates of the centroid G of angle ABC. Also, find the equation of a line passing through G and parallel to AB.

Sol. Let A( –4, 2), B(2, 6), C(8, 5) and D(9, – 7) be the vertices of the given quadrilateral. Let P, Q, R and S be the mid-points of AB, BC, CD and DA, respectively.
Then, the coordinates of P, Q, R and S are
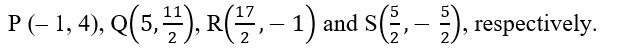
In order to prove that PQRS is a parallelogram, it is sufficient to show that PQ is parallel to RS and PQ = RS.
Here, slope of PQ,
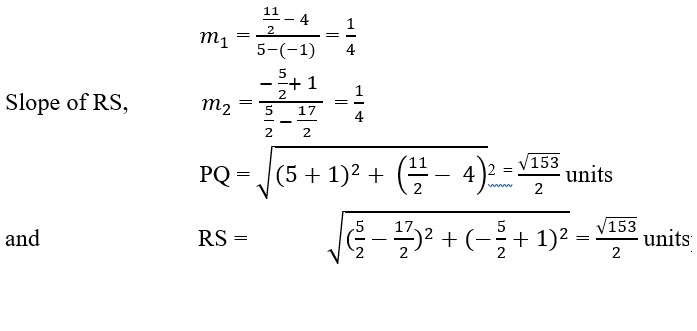
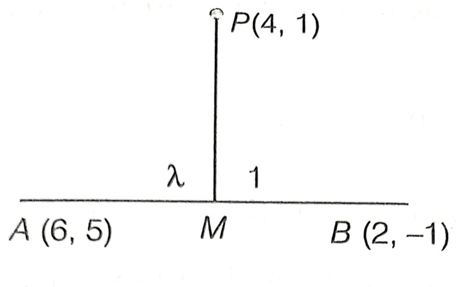
12. Show that the perpendicular drawn from the point (4, 1) on the line segment joining (6, 5) and (2, – 1) divides it internally in the ratio 8 : 5.
Sol. Let m be the slope of PM.

13. Given
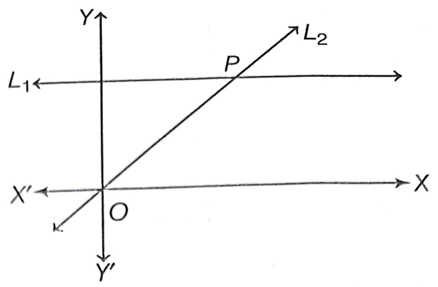
(i) Write the slope of line L2, if L2 is bisector of
(ii) Write the coordinates of point P.
(iii) Find the equation of L2.
Sol. (i) Given, L2 is the bisector of angle O.
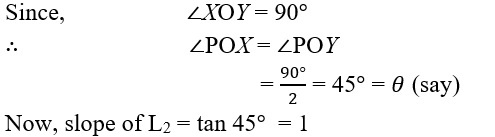
(ii) Let line L1 intersects Y-axis at M. Through P, draw a line parallel to Y-axis which intersect X-axis at N.
Then, clearly PN = OM = 4
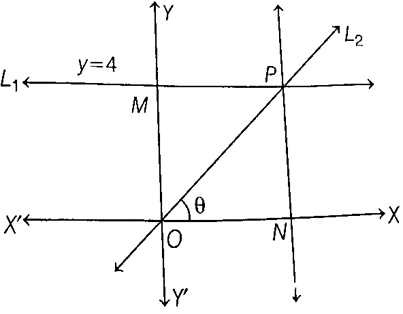

So, the coordinates of N are (4, 0) and the coordinates of M are (0, 4). Hence, the coordinates of P are (4, 4).
(iii) Equation of line L2, which is passing through origin (0, 0) and having slope 1, is

Hence, the required equation of L2 is y = x
14. A line AB meets X-axis at A and Y-axis at B point P(4, – 1) divides AB in the ratio
1 : 2. Find
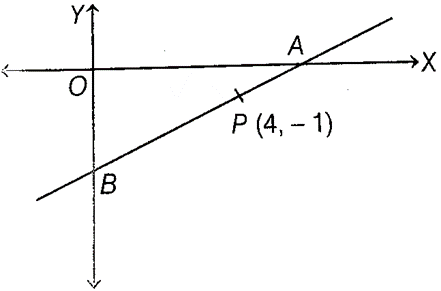
(i) the coordinates of A and B.
(ii) the equation of the line through P and perpendicular to AB.
Sol. (i) Let the coordinates of point A lying on X-axis be (x, 0) and the coordinates of point B lying on Y-axis be (0, y).

By using section formula,

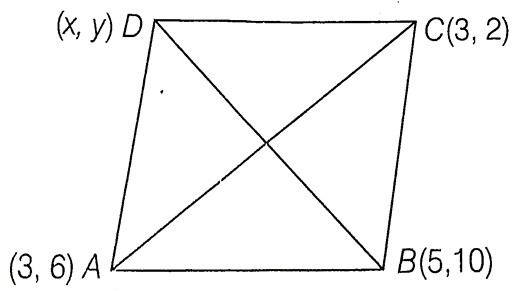
15. Three vertices of a parallelogram ABCD taken in order are A(3, 6), B(5, 10) and C(3, 2). Find
(i) the coordinates of the fourth vertex D.
(ii) the length of diagonal BD.
(iii) the equation of side AB of the parallelogram ABCD.
Sol. (i) Let the coordinates of vertex D be (x, y).
Since, ABCD is a parallelogram and we know that diagonals bisect each other in a parallelogram. So, the mid-point of AC and mid-point of BD are same.

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: EQUATION OF LINE CLASS 10 ICSE NOTES
ALSO VISIT:
10th ICSE
| Also Learn: | Attempt theQuiz on Mathematics : | Attempt theQuiz on Physics: | Attempt theQuiz on Biology: | Attempt theQuiz on Chemistry: |
| 1.Surface Areas and Volumes 2. ELECTRICITY 3. METALS AND NON METALS 4. ATOMS AND MOLECULES 5. GST 6. PHOTOSYNTHESIS IN HIGHER PLANTS 7. ABSORPTION BY ROOTS 8. QUADRATIC EQUATIONS 9. LINEAR INEQUATIONS 10. RECURRING DEPOSIT 11. CIRCULAR MOTION 12. MCQ WORK POWER ENERGY 13. ACIDS BASES AND SALTS 14. MCQ ON ACIDS BASES AND SALTS 15. ROTATIONAL MOTION MASS 2 16. ROTATIONAL MOTION MASS 1 17. MCQ ON PERIODIC TABLE 2 18. MCQ ON PERIODIC TABLE 1 19. CELL CYCLE AND CELL DIVISION 20.REFLECTION CLASS 10 ICSE NOTES | QUIZ ON SURFACE AREAS AND VOLUMES- MATHEMATICS QUIZ ON SECTION AND MID-POINT | QUIZ ON ELECTRICITY- PHYSICS | QUIZ 1 ON METALS AND NON-METALS – CHEMISTRY QUIZ 2 ON METALS AND NON-METALS – CHEMISTRY |
