DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
Table of Contents
ICSE CLASS 10 PROBABILITY QUESTIONS
1. What is the resulting sample space, if
(i) one coin is tossed?
(ii) two coins are tossed simultaneously?
(iii) three coins are tossed simultaneously?
Sol. (i) When a coin is tossed, then possible outcomes are H and T.
(ii) When two coins are tossed, then possible outcomes are
(HH), (HT), (TH) and (TT).
(iii) When three coins are tossed, then possible outcomes are (HHH), (HHT), (HTH), (THH), (THT), (TTH), (HTT) and (TTT).
2. A die is thrown once. Find the probability of getting
(i) a prime number.
(ii) a number lying between 2 and 6.
(iii) an odd number.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
Sol. Here, number of possible outcomes = 6
(i) Let E₁ = Event of getting a prime number.
Then, E1 = {2, 3, 5}
n(E1) = 3
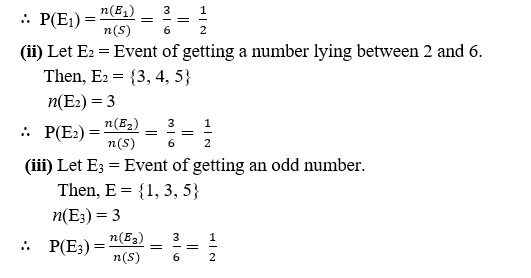
3. From a pack of 52 playing cards, whose numbers are multiples of 3 are removed. A card is now drawn at random. What is the probability that the card drawn is
(i) a face card (king, jack or queen)?
(ii) an even numbered red card?
Sol. Total number of cards in a pack = 52
Multiples of 3 in each suit are 3, 6 and 9.
We know that, in a pack of cards, there are four suits.
Number of cards removed = 34 = 12
Total number of cards left = 52 – 12 = 40
Let E1 be the event of a face card
(i) Number of favorable cards = 3X 4 = 12

4. Two players Neha and Shivani play a tennis match. It is known that the probability of Neha winning the match is 0.62. What is the probability of Shivani winning the match?
Sol. Let E and F denotes the events that Neha and Shivani win the match, respectively. It is clear that, if Neha wins the match, then Shivani losses the match and, if Shivani wins the match, then Neha losses the match. Thus, E and F are complementary events.
Since, probability of Neha’s winning the match,
i.e. P(E)=0.62
P(F) = P (Neha losses the match)
= 1-P(E) [P(E) + P(F) = 1]
= 1-0.62 = 0.38
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
5. Savita and Hamida are friends. What is the probability that both will have
(i) the same birthday?
(ii) different birthdays? (ignoring a leap year)
There are 365 days in a year, so Savita’s birthday can be at any day of 365 days in the year.
Similarly, Hamida’s birthday can be at any day of 365 days in the year.
So, total number of possible outcomes = 365 X 365
(i) If both have same birthday, then the number of outcomes favourable for their birthday = 365
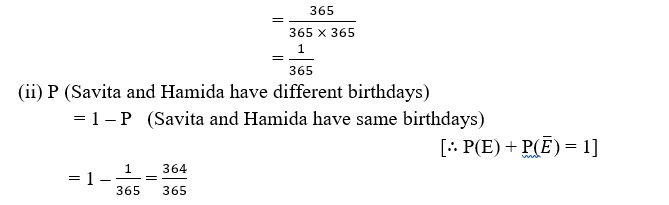
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
6. 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Sol. Total number of pens = 12 defective pens + 132 good pens
= 144 pens
Let E be the event of selecting a good pen.
Then, number of outcomes favourable to E = 132
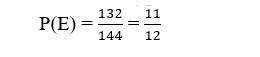
7. An integer is chosen between 0 and 100. What is the probability that it is
(i) divisible by 7?
(ii) not divisible by 7?
Sol. The total number of integers between 0 and 100 is 99.
(i) Let E1 = Event of choosing an integer which is divisible by 7
= {7, 14, 21, 28, 35, 42 49, 56, 63, 70, 77, 84, 91, 98)
Then, number of outcomes favourable to E = 14

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
8. In a musical chair game, the person playing the music has been advised to stop playing the music at any time within 2 min after she starts playing. What is the probability that the music will stop within the first half-minute after starting?
Sol. Since, the music is stopped at any time within 2 min.
So, the possible outcomes are all real numbers (representing minute) between 0 and 2 which are represented on the number line.
Let E be the event that the music is stopped within the first half-minute. Then, outcomes favourable to E are points on the number line from 0 to 1/2.

Here, all the outcomes are equally likely.
= Total distance from 0 to 2 = 2
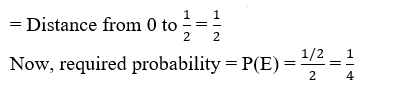
(i) a non-leap year.
(ii) a leap year.
Sol. (i) In non-leap year, there are 365 days, out of which 364 days make 52 weeks and in each week there is one Sunday,
Therefore, we have to find probability of having a Sunday on the remaining 1 day. Now, that I day can be Monday, Tuesday, Wednesday, Thursday, Friday, Saturday and Sunday.
P(a non leap year) = 1/2
(ii) In a leap year, there are 366 days, out of which 364 days make 52 weeks and in each week there is one Sunday. Therefore, we have to find the probability of having a
Sunday on one of the remaining 2 days.
Now, the 2 days can be (Sunday, Monday) or (Monday, Tuesday) or (Tuesday, Wednesday) or (Wednesday, Thursday) or (Thursday, Friday) or (Friday, Saturday) or (Saturday, Sunday). Note that Sunday occurs 2 times in these 7 pairs.
P(a leap year) =2/7
 10. Cards bearing numbers 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 are kept in a bag. A card is drawn at random from the bag. Find the probability of getting a card which is
10. Cards bearing numbers 2, 4, 6, 8, 10, 12, 14, 16, 18 and 20 are kept in a bag. A card is drawn at random from the bag. Find the probability of getting a card which is(i) a prime number.
(ii) a number divisible by 4.
(iii) a number that is a multiple of 6. mil (HD)
(iv) an odd number.
Sol. Let E₁, E₂, E3 and E, is the event of getting a card which is a prime number, a number divisibly by 4, a number that is a multiple of 6 and an odd number, respectively.
Total number of outcomes = 10
(i) Number of favourable outcomes (prime numbers) = 1

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
11. 16 cards are labelled as a, b, c,…, m, n, o, p. They are put in a box and shuffled. A boy is asked to draw a card from the box. What is the probability that the card drawn is
(i) a vowel?
(ii) a consonant?
(iii) none of the letters of the word ‘median’?
Sol. Total number of cards = 16
Clearly, the cards labelled a, e, i, o are vowels and rest 12 are consonant.
(i) There are 4 ways of drawing a vowel card.

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
12. A lot consists of 48 mobile phones of which 42 are good, 3p have only minor defect and 3 have major defect. Varnika will buy a phone, if it is good but the trader will only buy a mobile, if it has no major defect. One phone is selected at random from the lot. What is the probability that it is
(i) acceptable to Varnika?
(ii) acceptable to the trader?
Sol. Given, total number of mobile phones is 48.
So, number of possible outcomes = 48


DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
13. Three-digit numbers are made using the digits 4, 5, 9 (without repetition). If a number among them is selected at random, then what is the probability that the number will
(i) be a multiple of 5?
(ii) be a multiple of 9?
(iii) end with 9?
Sol. Here, three-digit numbers made from the digits 4, 5, 9, (without repetition) are 459, 495, 549, 594, 945, 954.
The sample space has 6 equally likely outcomes.
(i) Let E be the event of getting a multiple of 5, then E = {495, 945}.
So, number of outcomes favourable to E = 2

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
14. If 65% of the population have black eyes, 25% have brown eyes and the remaining have blue eyes, then what is the probability that a person selected at random has
(i) blue eyes?
(ii) brown or black eyes?
(iii) neither blue nor brown eyes?
Sol. Given, 65% of the population have black eyes, 25% have brown eyes and the remaining (100-65-25) %, i.e. 10% have blue eyes.
Let the total number of people be 100, then 65 have black eyes, 25 have brown eyes and 10 have blue eyes. Therefore, the sample space of the experiment has 100 equally likely outcomes.
(i) Let the event be have blue eyes’. As 10 people have blue eyes.
So, the number of outcomes favourable to the event have blue eyes’ = 10.

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
15. A child’s game has 8 triangles of which 3 are blue and rest are red, and 10 squares of which 6 are blue and rest are red. If one piece is lost at random, then find the probability that it is a
(i) triangle.
(ii) square
(iii) square of blue colour.
(iv) triangle of red colour.
Sol. A child’s game has 8 triangular pieces and 10 square pieces. So, total number of pieces in the game = 8+ 10 = 18.
One piece is lost at random means that all pieces are equally likely to be lost. Therefore, the sample space of the experiment has 18 equally likely outcomes.
(i) Number of triangular pieces = 8

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
ALSO VISIT:
10th ICSE
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: ICSE CLASS 10 PROBABILITY QUESTIONS
