NDA SETS PREVIOUS YEAR QUESTIONS – 35 PREVIOUS YEAR MCQs OF MATHEMATICS WITH ANSWERS- NATIONAL DEFENCE ACADEMY EXAMINATION

Leave a Comment / NDA / By admin

INTRODUCTION

This Practice Set for All Competitive Exams Make Important Roll For NDA, NAVY, AIRFORCE, and SAT. Important Practice Set for All Competitive Exams is Easy to Learn and Questions are Important for exam preparations. This topic is very important for above exams because every year approx 3-4 question are asking in each paper of NDA.   

Set and their representations

 A set is a well-defined collection of objects.

There are two methods of representing a set

(i) Roaster or tabular form (ii) Set builder form

The empty set  A set which does not contain any element is called the empty set or the void set or null set and is denoted by { } or φ.

NDA SETS PREVIOUS YEAR QUESTIONS

Singleton Set

A set which does not contain any element is called the Singleton set .

Finite and infinite sets A set which consists of a finite number of elements is called a finite set otherwise, the set is called an infinite set.

Cardinal number The number of elements in finite set is represented by n(A), known as Cardinal number.

Subsets A set A is said to be a subset of set B if every element of A is also an element of B. In symbols we write A ⊂ B if a ∈ A ⇒ a ∈ B.

We observe that N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, Q ⊄ T, N ⊄ T

Note: The set is also a subset of itself.

If A is not a subset of B, then it is denoted as A⊄B.

If A is a set with n(A) = m, then the number of subsets of A are 2^m and the number of proper subsets of A are 2^m -1.

Equivalent set

If the number of elements is the same for two different sets, then they are called equivalent sets. The order of sets does not matter here. It is represented as:

 n(A) = n(B)

where A and B are two different sets with the same number of elements.

 Equal sets

Given two sets A and B, if every elements of A is also an element of B and if every element of B is also an element of A, then the sets A and B are said to

be equal. The two equal sets will have exactly the same elements.

Intervals as subsets of R Let a, b ∈ R and a < b. Then

(a) An open interval denoted by (a, b) is the set of real numbers {x : a < x < b}

(b) A closed interval denoted by [a, b] is the set of real numbers {x : a ≤ x ≤ b)

(c) Intervals closed at one end and open at the other are given by

[a, b) = {x : a ≤ x < b} (a, b] = {x : a < x ≤ b}

Power set The collection of all subsets of a set A is called the power set of A.

NDA SETS PREVIOUS YEAR QUESTIONS

It is denoted by P(A). If the number of elements in A = n , i.e., n(A) = n, then the number of elements in P(A) = 2ⁿ.

Universal set This is a basic set; in a particular context whose elements and subsets are relevant to that particular context. For example, for the set of vowels in English alphabet, the universal set can be the set of all alphabets in English. Universal set is denoted by U.

Venn diagrams Venn Diagrams are the diagrams which represent the relationship between sets. For example, the set of natural numbers is a subset of set of whole numbers which is a subset of integers. We can represent this relationship through Venn diagram in the following way

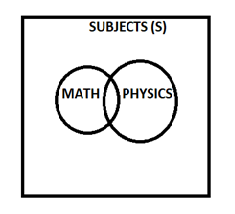
 OPERATIONS ON SETS

 UNION OF TWO SETS

The union of two sets A and B, written as A ∪ B (read as “A union B”), is the set consisting of all the elements which are either in A or in B or in both Thus,

A ∪ B = {x : x _∈ A or x _∈ B}

Clearly, x _∈ A ∪ B à x _∈ A or x _∈ B, and

xÏ A ∪ B à x Ï A and x Ï B.

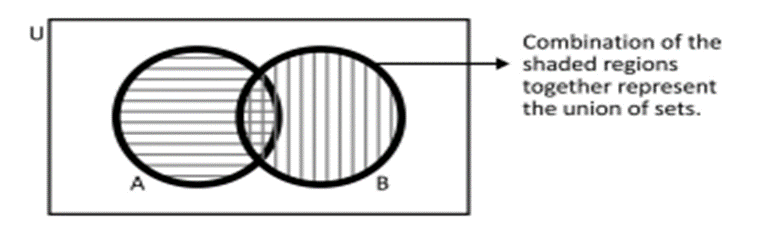
For example, if A={a, b, c, d} and B= {c, d, e, f}, then AUB = {a, b, c, d, e, f}

NDA SETS PREVIOUS YEAR QUESTIONS

Intersection of Two sets

The intersection of two sets A and B, written as A ∩ B (read as ‘A’ intersection ‘B’) is the set consisting of all the common elements of A and B. Thus,

A ∩ B = {x : x ∈ A and x ∈ B}

Clearly, x ∈ A∩B →x ∈ A and x ∈ B, and x ÏA∩B à xÏA or x ÏB.

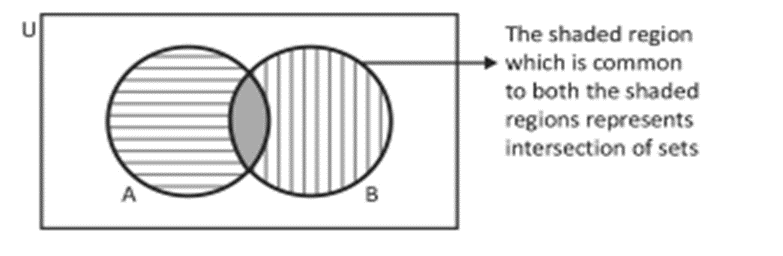
For example, if A = {a, b, c, d) and B = {c, d, e, f}, then A ∩ B = {c, d}.

Disjoint Sets

Two sets A and B are said to be disjoint, if A ∩ B = ɸ , i.e. A and B have no element in common.

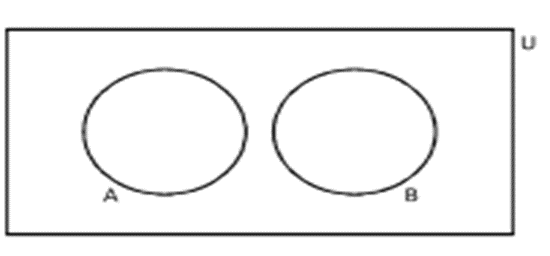
For example, if A = {1, 3, 5} and B = {2, 4, 6}, then A ∩ B = ɸ , so A and B are disjoint sets

NDA SETS PREVIOUS YEAR QUESTIONS

Difference of Two Sets

If A and B are two sets, then their difference A – B is defined as :

A – B = {x : x ∈ A and x Ï B}.

Similarly, B – A = {x : x ∈ B and x ÏA }.

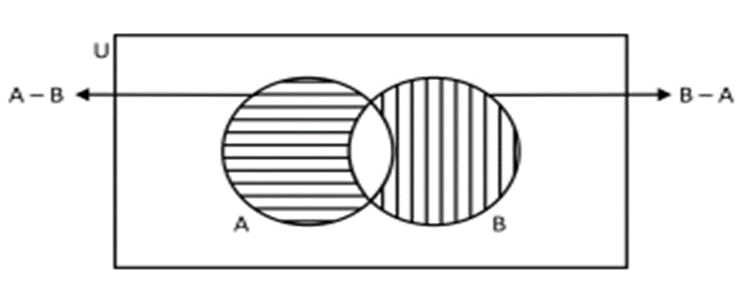
For example, if A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7, 9} then A – B = {2, 4} and B – A = {7, 9}.

Important Results

(a) A – B ≠ B – A

(b) The sets A – B , B – A and A ∩ B are disjoint sets

(c) A – B  ⊆ A and B – A ⊆ B

(d) A – ɸ = A and A – A = ɸ

 Symmetric Difference of Two Sets

The symmetric difference of two sets A and B , denoted by A ∆ B, is defined as

A ∆ B = (A – B) ∪ (B – A).

For example, if A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7, 9}

 then A ∆ B = (A – B) ∪ (B – A) = {2, 4} ∪ {7, 9} = {2, 4, 7, 9}.

 Complement of a Set

5. ALGEBRA OF SETS

1. For any set A , we have

a) A ∪ A = A                                      b) A ∩ A = A

2. For any set A, we have

a) A ∪ ɸ = A                                      b) A ∩ = ɸ = ɸ

c) A ∪ U = U                                    d) A ∩ U = A

3. For any two sets A and B, we have

a) A ∪ B = B ∪ A                               b) A ∩  B = B ∩ A

4. For any three sets A, B and C, we have

a) A ∪ (B ∪ C) = (A ∪ B) ∪ C             b) A ∩ (B ∩ C) = (A ∩ B) ∩ C

5. For any three sets A, B and C, we have

a) A ∪ (B ∩ C) = (A ∪ B) ∩  (A ∪ C)

b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)

NDA SETS PREVIOUS YEAR QUESTIONS

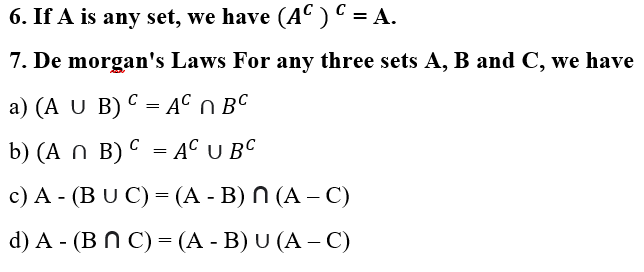
NDA( 2021)Paper 2

1. Consider the following statements in respect of sets:

1. The union over intersection of sets is distributive.

2. The complement of union of two sets is equal to intersection of their complements.

3. If the difference of two sets is equal to empty set, then the two sets must be equal.

Which of the above statements are correct?

(a) 1 and 2 only

(b) 2 and 3 only

(c) 1 and 3 only

(d) 1, 2 and 3

• Consider three sets X, Y and Z having 6, 5 and 4 elements respectively. All these 15 elements are distinct.

Let S = (X –Y) ∪ Z. How many proper subsets does S have?

(a) 255          

(b) 256

(c) 1023                 

(d) 1024

• Suppose set A consists of first 250 natural numbers that are multiples of 3 and set B consists of first 200 even natural numbers. How many elements does A ∪ B have

(a) 324           

(b) 364 

(c) 384

(d) 400

NDA( 2021)Paper 1

• If A and B are two matrices such that AB is of order n × n, then which one of the following is correct?

(a) A and B should be square matrices of same order.

(b) Either A or B should be a square matrix

(c) Both A and B should be of same order.

(d) Orders of A and B need not be the same.

• Consider the following statements:

1. The null set is a subset of every set.

2. Every set is in a subset of itself.

3. If a set has 10 elements, then its power set will have 1024 elements.

Which of the above statements are correct?

(a) 1 and 2 only

(b) 2 and 3 only

(c) 1 and 3 only

(d) 1, 2 and 3

• The numbers of Science, Arts and Commerce graduates working in a company are 30, 70 and 50 respectively. If these figures are represented by a pie chart, then what is the angle corresponding to Science graduates?

(a) 36 °

(b) 72°

(c) 120 °

(d) 168°

• Consider the following statements :

1.     A = (1, 3, 5) and B = {2, 4, 7} are equivalent sets.

2.     A = (1, 5, 9) and B = (1, 5, 5, 9, 9) are equal sets.

Which of the above statements is / are correct?

(a) 1 only

(b) 2 only

 (c) Both 1 and 2

(d) Neither 1 nor 2

NDA( 2020)

NDA SETS PREVIOUS YEAR QUESTIONS

Directions for the following three (03) items:

 Consider the following Venn diagram, where X, Y and Z are three sets. Let the number of elements in Z be denoted by n(Z) which is equal to 90.

•  If the number of elements in Y and Z are in the ratio 4 : 5 , then what is the value of b?

(a) 18              (b) 19                  (c) 21                   (d) 23

•  What is the value of n(X) + n(Y) + n(Z) – n(X ∩ Y) – n(Y ∩ Z) –  n(X ∩ Z) + n(X ∩ Y ∩ Z)?

(a) a + b + 43                                       (b) a + b + 63

(c) a + b + 96                             (d) a + b + 106

1. If the number of elements belonging to neither X, nor Y, nor Z is equal to p, then what is the number of elements in the complement of X?

(a) p + b + 60                            

(b) p + b + 40

(c) p + a + 60

(d) p + a + 40

NDA 2019 Paper1

1. Let X be a non-empty set and let A, B, C be subsets of X. Consider the following statements:

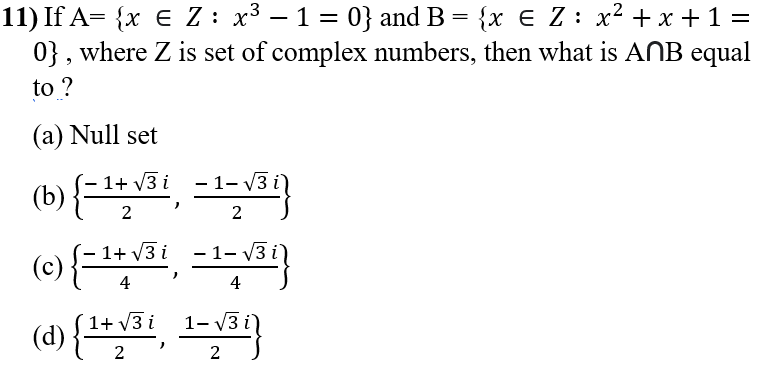
1. A ⊂ C à (A ∩ B) ⊂ (C ∩ B) (A ∪ B) ⊂ (C ∩ B)

2. (A ∩ B) ⊂ (C ∩ B) for all sets B à A ⊂ C

3. (A ∪ B) ⊂ (C ∪ B) for all sets B à A ⊂ C

Which of the above statements are correct?

(a) 1 and 2 only           (b) 2 and 3 only

(c) 1 and 3 only           (d) 1, 2 and 3

In a school, all the students play at least one three indoor games – chess, carrom and table tennis. 60 play chess, 50 play table tennis, 48 play carrom, 12 play chess and carrom, 15 play carrom and table tennis, 20 play table tennis and chess.

1. What can be the minimum number of students in the school?

(a) 123

(b) 111

(c) 95

(d) 63

1. What can be the maximum number of students in the school?

(a) 111

(b) 123

(c) 125

(d) 135

NDA 2019 Paper 2

1. If A, B and C are subsets of a given set, then which one of the following relations is not correct?

(a) A ∪ (A ∩ B) = A ∪ B

(b) A ∩ (A ∪ B) = A

(c) (A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)

(d) (A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)

1. If a set A contains 3 elements and another set B contains 6 elements, then what is the minimum number of elements that  (A ∪ B) can have?

(a) 3                          (b) 6                     (c) 8                     (d) 9

1. If A= {x : 0 ≤ x ≤ 2} and B = {y; y is a prime number}, then what is A ∩ B equal to ?

(a) Ø

(b) {1}

(c) {2}

(d) {1, 2}

1. Let AUB={x | (x – a)(x – b) > 0, where a < b}. What are A and B equal to ?

(a) A = {x | x > a} and B = {x | x > b}

(b) A = {x | x < a} and B = {x | x > b}

(c) A = {x | x < a} and B = {x | x < b}

(d) A = {x | x > a} and B = {x | x < b}

• Let S = {2, 4, 6, 8, ………………..20}. What is the maximum number of subsets does S have?

(a) 10

(b) 20

(c) 512

(d) 1024

NDA 2018 Paper 1

• Let A and B be subsets of X and C = (A ∩ B’) ∪ (A’ ∩ B), where A’ and B’ are complements of A and B respectively in X. What is C equal to ?

(a) (A ∪ B’) – (A ∩ B’)

(b) (A ∪ B) – (A ∩ B)

(c) (A ∪ B) – (A ∩ B)

(d) (A’ ∪ B’) – (A’ ∩ B’)

NDA SETS PREVIOUS YEAR QUESTIONS

Consider the information given below and answer the two items (02) that follow :

In a class, 54 students are good in Hindi only. 63 students are good in Mathematics only and 41 students are good in English only. There are 18 students who are good in both Hindi and Mathematics. 10 students are good in all three subjects.

• What is the number of students who are good in either Hindi or Mathematics but not in English?

(a) 99                                

(b) 107

(c) 125 

(d) 130

• What is the number of students who are good in Hindi and Mathematics but not in English?

(a) 18

(b) 12

(c) 10   

(d) 8

• A survey of 850 students in a university yield that 680 students like music and 215 like dance. What is the least number of students who like both music and dance?

(a) 40

(b) 45

(c) 50

(d) 55

NDA 2018 Paper 2

NDA SETS PREVIOUS YEAR QUESTIONS

Consider the information given below and answer the two (02) items that follow:

A survey was conducted 300 students It was found that 125 students like to play cricket, 145 students like to play football and 90 students like to play tennis 32 students like to play exactly two games out of the three Games.

• How many students like to play all the three games.

     (a) 14             (b) 21                  (c) 28                   (d) 35

• How many students like to play exactly only one game?

      (a) 196          (b) 228                (c) 254                (d) 268

2017 NDA Paper 1

• Let S be the set of all persons living in Delhi We say that x, y in S are related if they were born in Delhi on the same day. Which one of the following is correct?

(a) The relation is an equivalent relation

(b) The relation is not reflexive but it is symmetric and transitive

(c) The relation is not symmetric but it is reflexive and transitive

(d) The relation is not transitive but it is reflexive and symmetric

• Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Then the number of subsets of A containing two or three elements is

(a) 45                   (b) 120                (c) 165                (d) 330

• Consider the following in respect of sets A and B :

1. (A – B) ∪ B = A

2. (A – B) ∪ A = A

3. (A – B) Ç B = ɸ

4. A ⊆ B ð$ A ∪ B = B

Which of the above are correct?

(a) 1, 2 and 3

(b) 2, 3 and 4

(c) 1, 3 and 4

(d) 1, 2 and 4

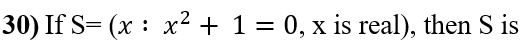
(a) {- 1}              (b) {0}                (c) {1}                 (d) an empty set

NDA 2017 Paper -2

• If E is the universal set and A = B ∪ C, then

 the set E – (E – (E – (E – (E – A)))) is same as the set

(a) B’ ∪ C’                  

(b) B ∪ C

(c) B’ ∩ C’

(d) B ∩ C

• If A = (x : x is a multiple of 2}, B = (x : x is a multiple of 5} and C= {x : x is a multiple of 10}, then A ∩ (B ∩ C) is equal to

(a) A

(b) B

(c) C

(d) {x : x is a multiple of 100}

NDA 2016 Paper -2

NDA SETS PREVIOUS YEAR QUESTIONS

• Let S be a set of all distinct numbers of the form p/q , where p, q e {1,2,3,4,5,6}. What is the cardinality of set S?
• 21
• 23
• 32
• 36
• If A= {x e R: x² + 6x -7<0} and                                        B= { x e R : x² + 9x +14>0}, then which of the following is/are correct ?
•  A Ç B ={x e R :  -2<x<1}
• A \ B ={x e R :  -7<x<-2}

Select the correct answer using the code given below :

• 1 only
• 2 only
• Both 1 and 2
• Neither 1 nor 2
• In an examination, 70% students passed in Physics, 80% passed in Chemistry, 75% students passed in Mathematics and 85 % students passed in biology, and x% students failed in all four subjects. What is the minimum value of x ?
• 10
• 12
• 15
• None of the above
  NDA SETS PREVIOUS YEAR QUESTIONS
• ANSWER KEYS

1	2	3	4	5	6	7	8	9	10
d	c	a	C	d	b	c	c	d	a
11	12	13	14	15	16	17	18	19	20
c	a	c	b	b	a	d	c	b	d
21	22	23	24	25	26	27	28	29	30
c	c	d	b	a	c	a	c	b	d
31	32	33	34	35
c	c	b	c	d