DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES
Table of Contents
SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES

Sol. Given, a line segment joining A(4, – 5) and B(4, 5) such that
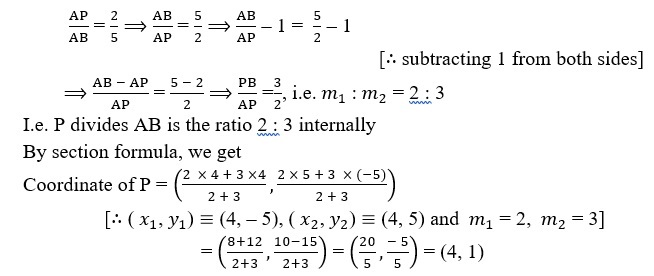
Hence, the coordinates of P are (4, – 1)
2. If P(9a – 2 – b) divides the line segment joining A(3a +1, – 3) and B(8a, 5) in the ratio 3: 1. Find the values of a and b.
Sol. Let(9a – 2, – b) divides AB internally in the ratio 3 : 1.
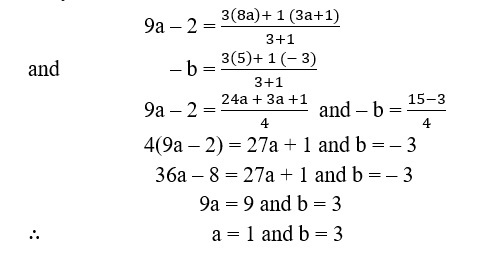
3. If two adjacent vertices of a parallelogram are (3, 2) and (– 1, 0) and the diagonals intersect at
(2, –5), then find the other two vertices.
Sol. Let two other coordinates be (x, y) and (x’’, y’’), respectively.
Using mid-point formula, we get
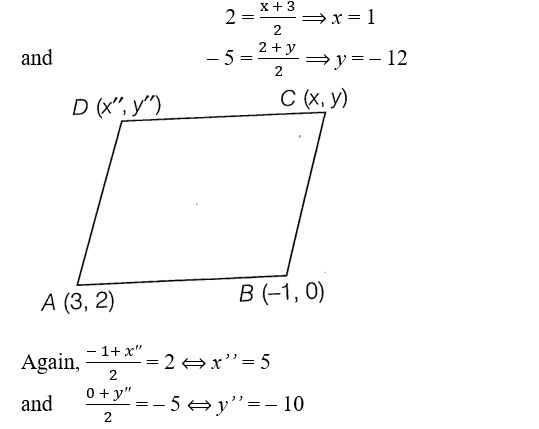
Hence, coordinates of C(1, – 12) and D(5, – 10).
4. If two vertices of a parallelogram are (2, 3) and Land (0, –1) and the diagonals cut at (2, –5), then find the other vertices of the parallelogram.
Sol. Let coordinates of C be
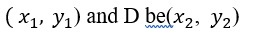

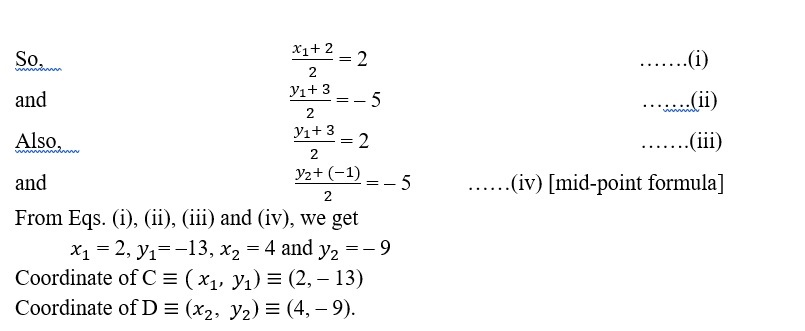
5. Find the mid-point of the line segment joining the points (3, –1) and (7, 9).
Sol. Let C(x, y) be the mid-point of the line joining the points A(3, – 1) and B(7, 9)
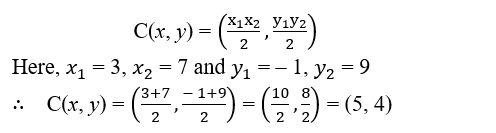
Hence, the mid-point of line segment joining (3, – 1) and (7, 9) is (5, 4).
6. Show that A(–1,0), B(3, 1), C(2, 2) and D(–2, 1) are the vertices of a parallelogram ABCD.
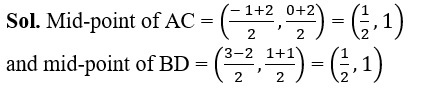
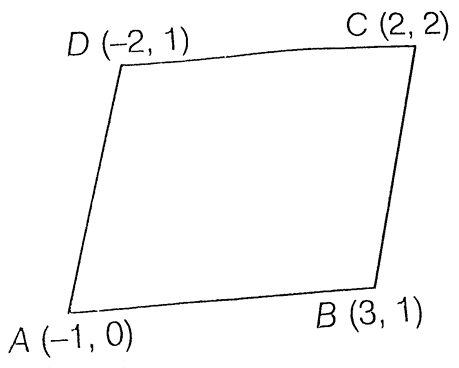
Since, diagonals of a quadrilateral bisect each other.
7. If the points A (6, 1), B (8, 2), C(9, 4) and D (p, 3) are the vertices of a parallelogram, taken in order, then find the value of p.
Sol. Given, vertices of a parallelogram are A(6, 1), B(8, 2), C(9, 4) and D(p, 3).

 Coordinate of mid-point of diagonal AC
Coordinate of mid-point of diagonal AC= Coordinate of mid-point of diagonal BD
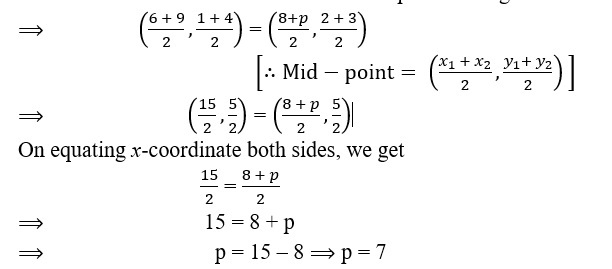
Hence, the required value of p is 7.
8. The line segment joining A(2, 3) and B(6, –5) is intersected by the X-axis at the point K. Write the coordinate of the point K. Find the ratio in which K divides AB.
Sol. Let K divides the line segment joining the points

By section formula, we get

9. A point P divides the line joining A (− 4, 1) and OITU: B (17, 10) in the ratio 1:2.
(i) Calculate the distance OP, where O is the origin.
(ii) In what ratio, does the Y-axis divide the line AB?
Sol. (i) Given, points are A (– 4, 1) and B(17, 10) and ratio = 1 : 2
Let the coordinate of P be (x, y)

10. In the figure given below, the line segment AB meets X-axis at A and Y-axis at B. The point
P (–3, 4) on AB divides it in the ratio 2 : 3. Find the coordinates of A and B.
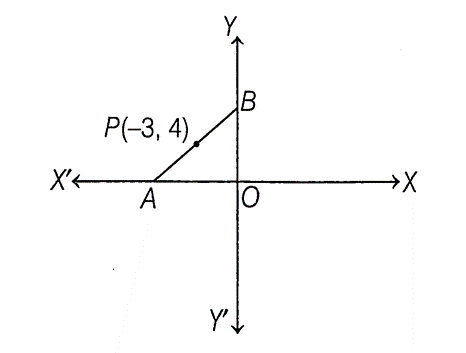
Sol. Let coordinate of A and B be A (– x, 0) and B(0, y).
Now, P (– 3, 4) on AB in the ratio 2 : 3.
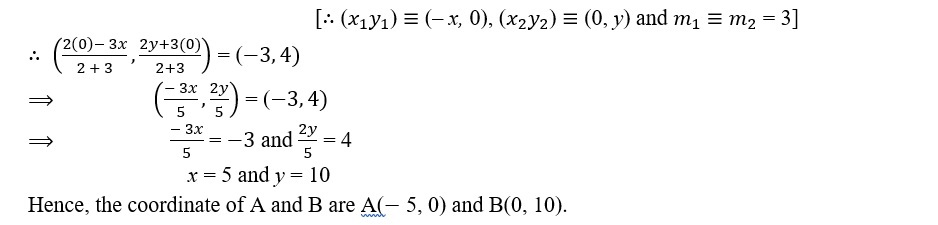
11. Find the coordinates of the points of trisection of the line segment joining (2, –3) and (4, –1).
Sol. Let P and Q be the points of trisection as shown below

Then, AP : PB = 1 : 2 and AQ : QB = 2 : 1

12. If A (2, 5), B(–1, 2) and C (5, 8) are the vertices of a AABC. P and Q are points on AB and AC respectively, such that AP: PB = AQ: QC = 1 : 2
(i) Find the coordinates of P and Q.

Hence, coordinate of Q will be (3, 6)
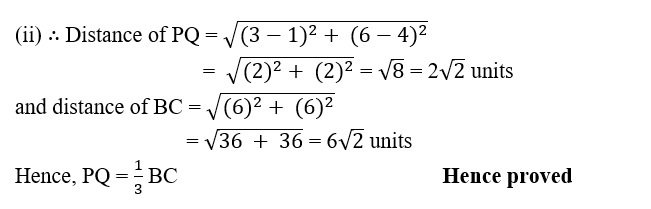
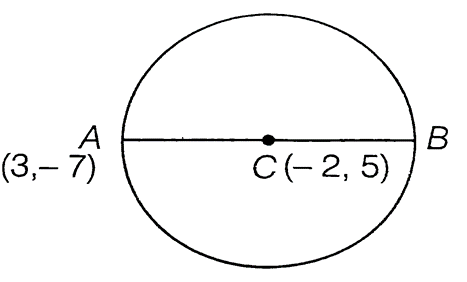
13. If AB is a diameter of a circle with centre C(–2,5) and A(3, –7). Find
(i) the length of radius AC.
(ii) the coordinate of B.

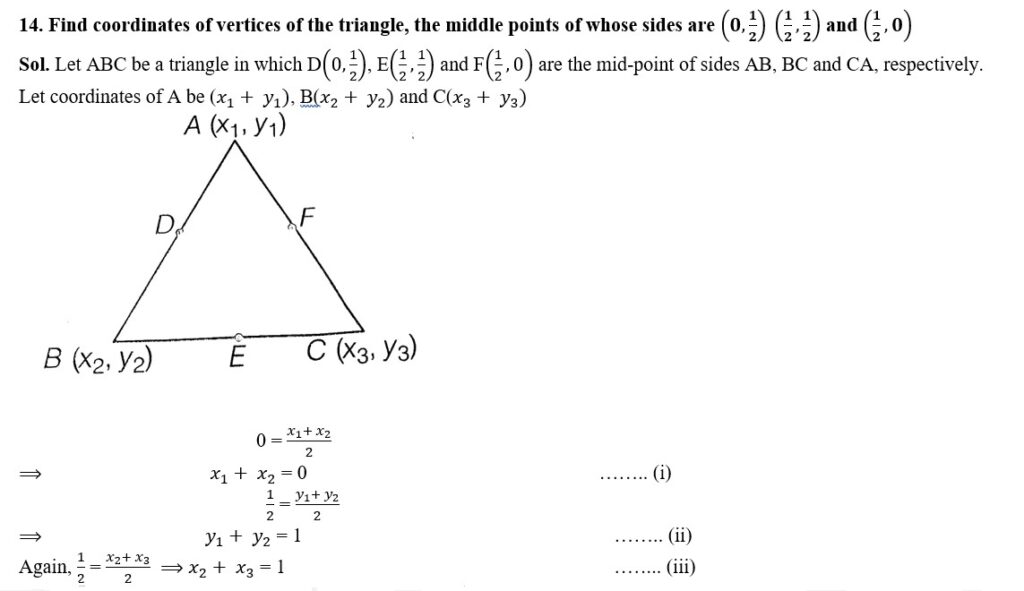

Coordinates of A, B and C will be (0, 0), (0, 1) and (1, 0).
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES
15. ABC is a triangle and G(4, 3) is the centroid9o21 of the triangle. If A(1, 3), B(4, b) and C (a, 1), then find a and b. Find the length of side BC.
Sol. Given, vertices and centroid of a triangle are A(1, 3), B(4, b), C(a, 1) and G(4, 3)
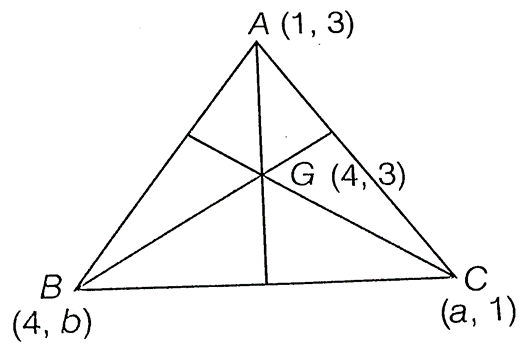
We know that, coordinates of centroid of the triangle,

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES
ALSO VISIT:
10th ICSE
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SECTION AND MID POINT FORMULA CLASS 10 ICSE NOTES
