DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
Set is a well-defined collection of objects. The objects belonging to a set are called elements or members of the set. Sets are usually denoted by capital letters of English alphabets while the elements are denoted in general, by small letters.
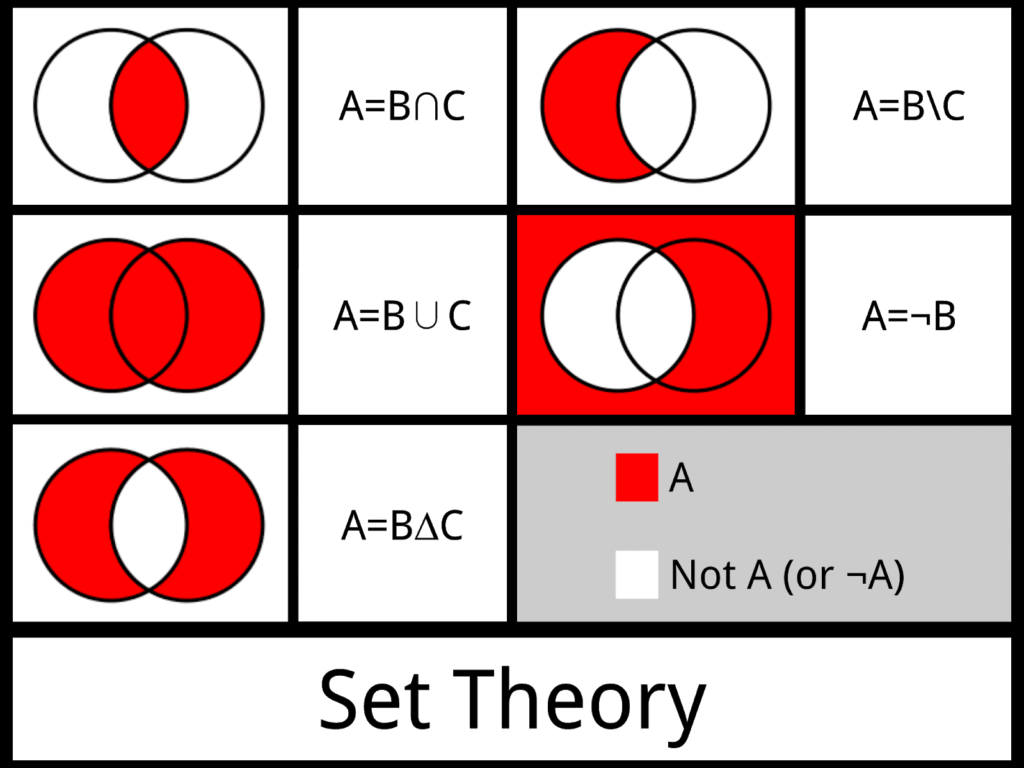
OPERATIONS ON SETS
1. UNION OF TWO SETS
The union of two sets A and B, written as A ∪ B (read as ‘A union B’), is the set consisting of all the elements which are either in A or in B or in both Thus,
A ∪ B = {x : x ∈ A or x ∈ B}
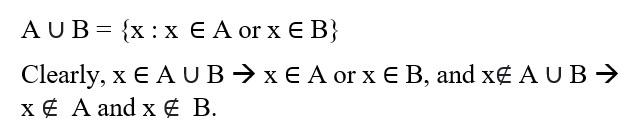
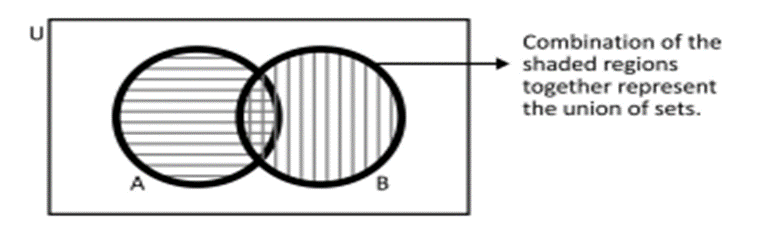
For example, if A = {a, b, c, d} and B = {c, d, e, f}, then A B = {a, b, c, d, e, f}
2. Intersection of Two sets
The intersection of two sets A and B, written as A ∩ B (read as ‘A’ intersection ‘B’) is the set consisting of all the common elements of A and B. Thus,
A ∩ B = {x : x ∈ A and x ∈ B}
Clearly, x ∈ A ∩ B → x ∈ A and x ∈ B, and x ∉ A ∩ B à x ∉ A or x ∉ B.
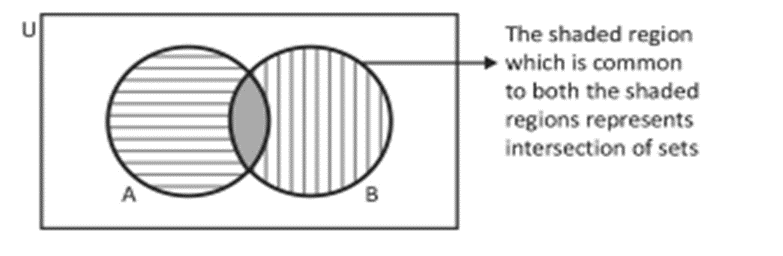
For example, if A = {a, b, c, d) and B = {c, d, e, f}, then A ∩ B = {c, d}.
3. Disjoint Sets
Two sets A and B are said to be disjoint, if A ∩ B = ɸ , i.e. A and B have no element in common.
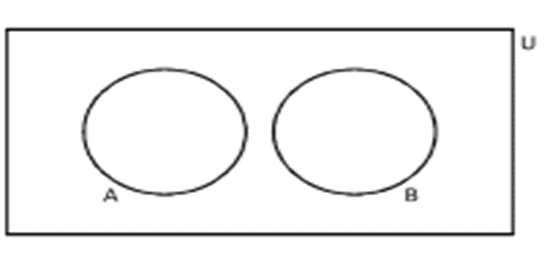
For example, if A = {1, 3, 5} and B = {2, 4, 6}, then A ∩ B = ɸ , so A and B are disjoint sets
4. Difference of Two Sets
If A and B are two sets, then their difference A – B is defined as :
A – B = {x : x ∈ A and x ∉ B}.
Similarly, B – A = {x : x ∈ B and x ∉ A }.
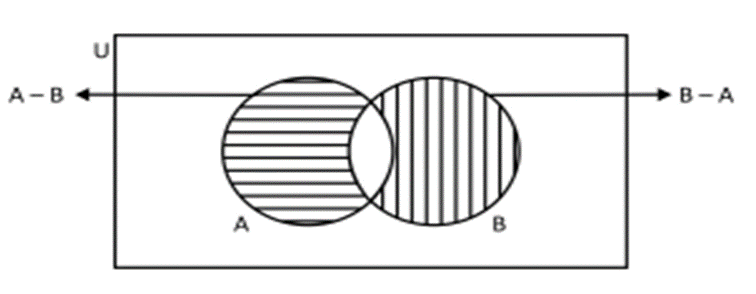
For example, if A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7, 9} then A – B = {2, 4} and B – A = {7, 9}.
Important Results
(a) A – B ≠ B – A
(b) The sets A – B , B – A and A ∩ B are disjoint sets
(c) A – B ⊆ A and B – A ⊆ B
(d) A – ɸ = A and A – A = ɸ
5. Symmetric Difference of Two Sets
The symmetric difference of two sets A and B , denoted by A ∆ B, is defined as
A ∆ B = (A – B) ∪ (B – A).
For example, if A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7, 9} then A ∆
B = (A – B) ∪ (B – A) = {2, 4} ∪ {7, 9} = {2, 4, 7, 9}.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
6. Complement of a Set

Important Results
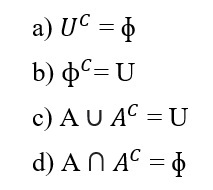
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
ALGEBRA OF SETS
1. For any set A , we have
a) A ∪ A = A
b) A ∩ A = A
2. For any set A, we have
c) A ∪ ɸ = A
d) A ∩ = ɸ = ɸ
e) A ∪ U = U
f) A ∩ = A
3. For any two sets A and B, we have
g) A ∪ B = B ∪ A
h) A ∩ B = B ∩ A
4. For any three sets A, B and C, we have
i) A ∪ (B ∪ C) = (A ∪ B) ∪ C
j) A ∩ (B ∩ C) = (A ∩ B) ∩ C
5. For any three sets A, B and C, we have
k) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
l) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
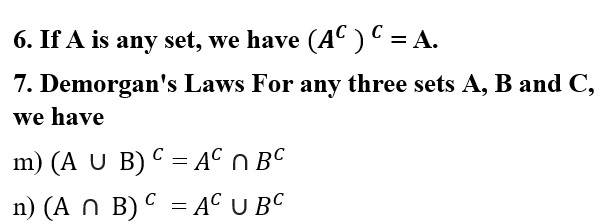
p) A – (B ∩ C) = (A – B) ∪ (A – C)
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
Table of Contents
SET THEORY JEE MAINS QUESTIONS
1. Let V = {a, e, i, o, u}, V –B = {e, o} and B –V = {k}.
Then, the set B is
(a) {a, i, u}
(b) {a, e, k, i}
(c) {a, i, k, u}
(d) (a, e, i, k, u}
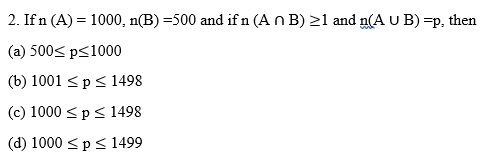
3. If n(A) =8 and n (A
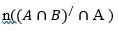
(a) 2
(b) 4
(c) 6
(d) 8
4. If the set A contains 5 elements, then the number of elements in the power set P (A) is equal to
(a) 32
(b) 25
(c) 16
(d) 8
5. In a certain town 25% families own a cell phone, 15% families own a scooter own scooter and 65% families own neither a cell phone nor a scooter. If 1500 families own both a cell phone and a scooter, then the total number of families in the town is
(a) 10,000
(b) 20,000
(c) 30,000
(d) 40,000
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
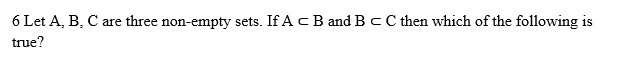
(a) B – A = C – B
(b) A ∩ B ∩ C = B
(c) A ∪ B = B ∩ C
(d) A ∪ B ∪ C = A
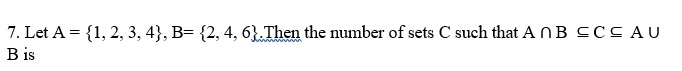
(a) 6
(b) 9
(c) 8
(d) 10
8. Let X and Y be the sets of all positive divisors of 400 and 1000 respectively (including 1 and the number). Then n (X∩Y) =
(a) 4
(b) 6
(c) 8
(d) 12

(a) 2
(b) 4
(c) 8
(d) 12
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
11. A class has 175 students. The following data shows the number of students opting one or more subjects. Maths – 100, Physics – 70, chemistry – 40, maths and physics -30, maths and chemistry – 28 physics and Chemistry -23, Maths, Physics and Chemistry – 18. How many have offered Maths alone?
(a) 35
(b) 48
(c) 60
(d) 22
12. Which of the following is true?
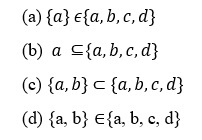
13. From 50 students taking examinations in subjects A, B and C, 37 passed A, 24 passed B and 43 passed C. Atmost 19 passed A and B, atmost 29 passed A and C and atmost 20 passed B and C. The largest possible number that could have passed all the three examinations is
(a) 15
(b) 16
(c) 17
(d) none of these
14. For sets A and B, which is false?
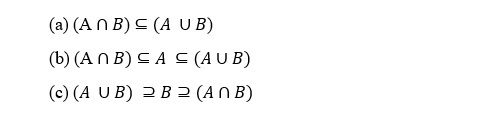
(d) A ∪ B can never be equal to A ∩ B
15. Which of the following is a null set?
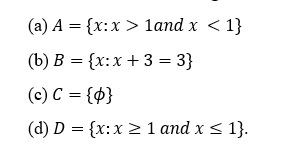
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
16. If ,then find which of the following statements are not true?

17. Let A and B be two non-empty subsets of a set X such that A is not a subset of B, then
(a) A is always a subset of the complement of B.
(b) B is always a subset of A
(c) A and B are always disjoint
(d) A and the complement of B are always non-disjoint
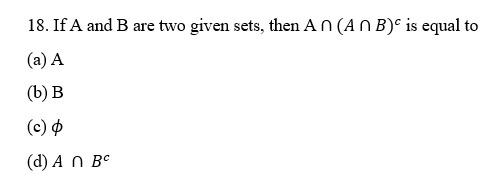
19. If A and B are non-empty sets, then P(A) ∪ P(B) is equal to
(a) P( A∪ B )
(b) P( A ∩ B )
(c) ɸ
(d) None of these
20. Out of 800 boys in a school, 224 played Cricket, 240 played Hockey and 336 played Basketball. Of the total, 64 played both Basketball and Hockey, 80 played Cricket and Basketball, 40 played Cricket and Hockey; 24 played all the three games. The number of boys who did not play any game is
(a) 128
(b) 216
(c) 240
(d) 160
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
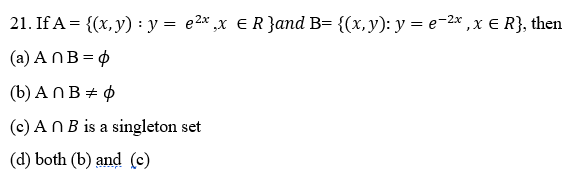

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
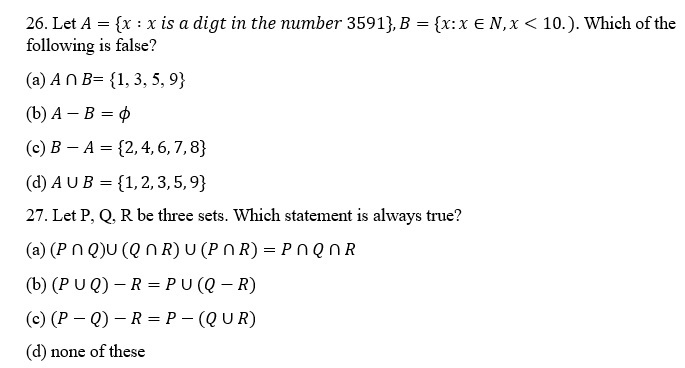
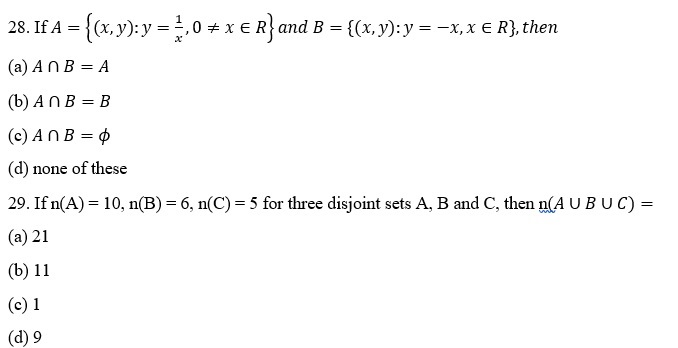
30. If n(A) = 4 and n(B) =7, then the minimum and maximum values of n(A ∪ B ) are respectively
(a) 4, 11
(b) 4, 7
(c) 7, 11
(d) none of these
31. If n(A) = 43, n(B) = 51 and n( A ∪ B )= 75 then = n( A – B ) ∪ ( B – A ))=
(a) 53
(b) 45
(c) 56
(d) 66
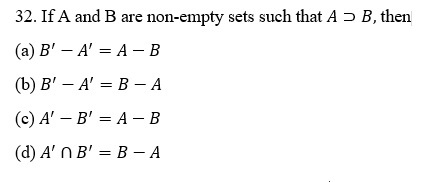
33. The shaded region in the figure represents
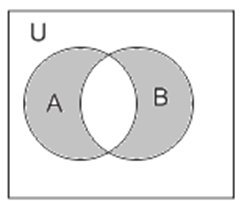
(a) A ∩ B
(b) A ∪ B
(c) B – A
(d) ( A – B ) ∪ ( B – A )
34. A market research group conducted a survey of 1000 consumers and reported that 720 consumers like product A and 450 consumers like the product B, then least number that must have like both products, is
(a) 730
(b) 170
(c) 180
(d) 1270
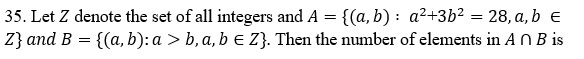
(a) 2
(b) 3
(c) 4
(d) 6


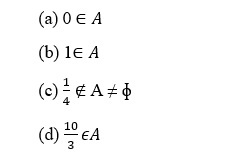
45.The set of intelligent students in a class is
(a) a null set
(b) a singleton set
(c) a finite set
(d) not a well defined collection

(a) 16
(b) 12
(c) 8
(d) 4
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS
ANSWERS:
| 1.C 2.D 3.C 4.A 5.C 6.C 7.C 8.D 9.B 10.C 11.C 12.C 13.D 14.D 15.A 16.A 17.D 18.D 19.D 20.D 21.D 22.B 23.B 24.C 25.A | 26.D 27.C 28.C 29.A 30.C 31.C 32.A 33.D 34.B 35.D 36.C 37.C 38.C 39.B 40.B 41.C 42.B 43.B 44.B 45.D 46.C 47.A 48.A 49.C 50.B |
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY CLASS 11 MCQ
ALSO VISIT :
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SET THEORY JEE MAINS QUESTIONS