DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
INTRODUCTION
This Practice Set for All Competitive Exams Make Important Roll For JEE-main (AIEEE), BITSAT, REAP, MHCET, and other STATE LEVEL ENGINEERING ENTRANCE EXAMS. Important Practice Set for All Competitive Exams is Easy to Learn and Questions are Important for exam preparations. This topic is very important for above exams because every year approx 1-2 question are asking in competitive exams.
Set and their representations
A set is a well-defined collection of objects.
There are two methods of representing a set
(i) Roaster or tabular form (ii) Set builder form
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
The empty set A set which does not contain any element is called the empty set or the void set or null set and is denoted by { } or φ.
Singleton Set
A set which does not contain any element is called the Singleton set .
Finite and infinite sets A set which consists of a finite number of elements is called a finite set otherwise, the set is called an infinite set.
Cardinal number The number of elements in finite set is represented by n(A), known as Cardinal number.
Subsets A set A is said to be a subset of set B if every element of A is also an element of B. In symbols we write A ⊂ B if a ∈ A ⇒ a ∈ B.
We observe that N ⊂ Z ⊂ Q ⊂ R, T ⊂ R, Q ⊄ T, N ⊄ T
Note: The set is also a subset of itself.
If A is not a subset of B, then it is denoted as A⊄B.
If A is a set with n(A) = m, then the number of subsets of A are 2m and the number of proper subsets of A are 2m -1.
Equivalent set
If the number of elements is the same for two different sets, then they are called equivalent sets. The order of sets does not matter here. It is represented as:
n(A) = n(B)
where A and B are two different sets with the same number of elements.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
Equal sets
Given two sets A and B, if every elements of A is also an element of B and if every element of B is also an element of A, then the sets A and B are said to
be equal. The two equal sets will have exactly the same elements.
Intervals as subsets of R Let a, b ∈ R and a < b. Then
(a) An open interval denoted by (a, b) is the set of real numbers {x : a < x < b}
(b) A closed interval denoted by [a, b] is the set of real numbers {x : a ≤ x ≤ b)
(c) Intervals closed at one end and open at the other are given by
[a, b) = {x : a ≤ x < b} (a, b] = {x : a < x ≤ b}
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
Power set The collection of all subsets of a set A is called the power set of A.
It is denoted by P(A). If the number of elements in A = n , i.e., n(A) = n, then the number of elements in P(A) = 2n.
Universal set This is a basic set; in a particular context whose elements and subsets are relevant to that particular context. For example, for the set of vowels in English alphabet, the universal set can be the set of all alphabets in English. Universal set is denoted by U.
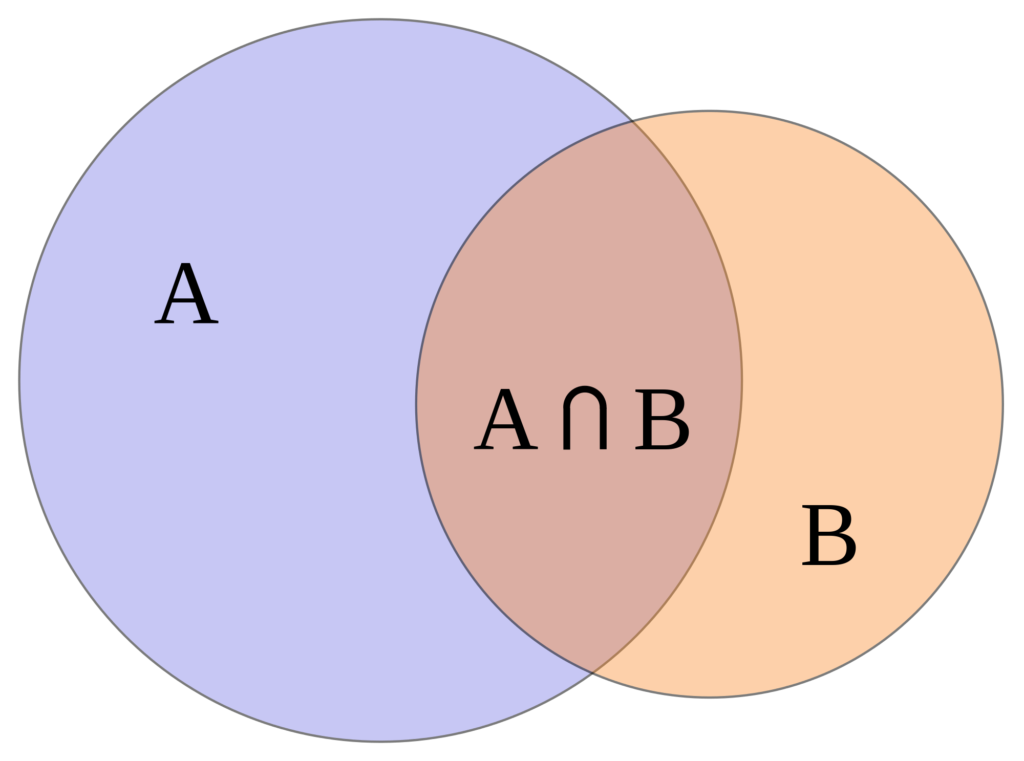
Venn diagrams Venn Diagrams are the diagrams which represent the relationship between sets. For example, the set of natural numbers is a subset of set of whole numbers which is a subset of integers. We can represent this relationship through Venn diagram in the following way
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS

OPERATIONS ON SETS
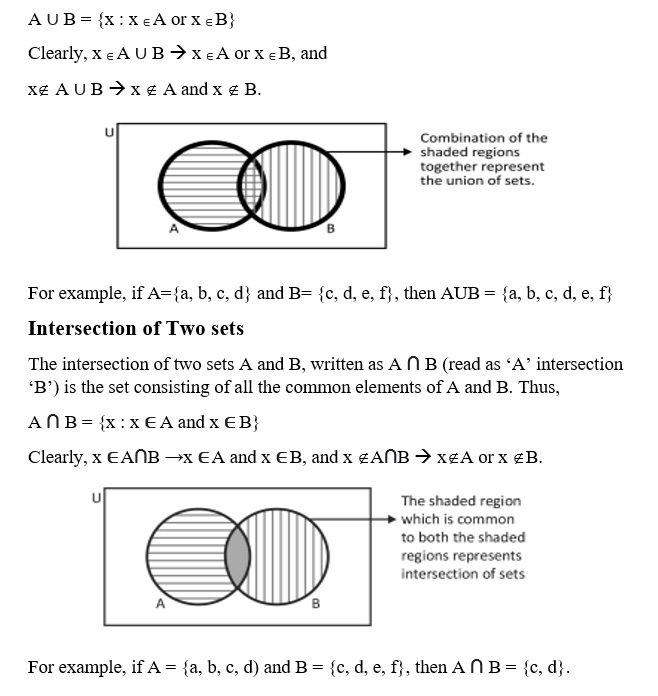
UNION OF TWO SETS
The union of two sets A and B, written as A ∪ B (read as “A union B”), is the set consisting of all the elements which are either in A or in B or in both Thus,
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS

(c) A – B ⊆ A and B – A ⊆ B
(d) A – ɸ = A and A – A = ɸ

5. For any three sets A, B and C, we have
a) A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
b) A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
Table of Contents
SETS QUESTIONS FOR JEE MAINS

4. If A = [-3, 7] and B = [2, 9], then which of the following is not true?
(a) A ∩ B = [2, 7]
(b) (A ∪ B)’ = (- ∞, – 3) (9, ∞)
(c) A – B = [ – 3, 2]
(d) A – B’ = [2, 7]
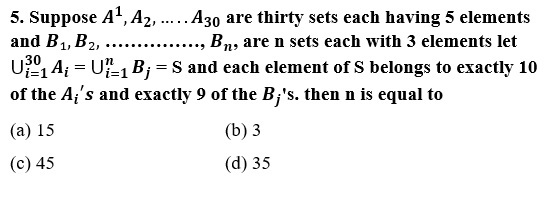
6. Two finite sets have m and n elements. The number of subsets of the first set is 112 more than that of the second set. The values of m and n are, respectively,
(a) 4, 7 (b) 7, 4
(c) 4, 4 (d) 7, 7
7. The set (A ∩ B)’ ∪ (B ∩ C) ‘ is equal to
(a) A‘ ∪ B ∪ C (b) A’ ∪ B
(c) A’ ∪ C’ (d) A’ Ç B
8. Let F1 be the set of parallelograms, F2 the set of rectangles, F3 the set of rhombuses, F4 the set of squares and F5 the set of trapeziums in a plane. Then F1, may be equal to
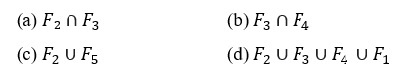
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS

10. Let R be set of points inside a rectangle of sides a and b (a, b > 1) with two sides along the positive direction of x – axis and y -axis. Then
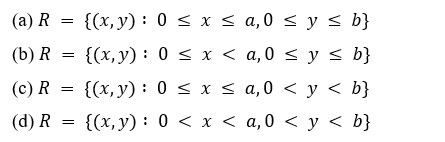
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
11. In a class of 60 students, 25 students play cricket and 20 play tennis, and 10 students play both games. Then, the number of students who play neither is
(a) 0 (b) 25
(c) 35 (d) 45
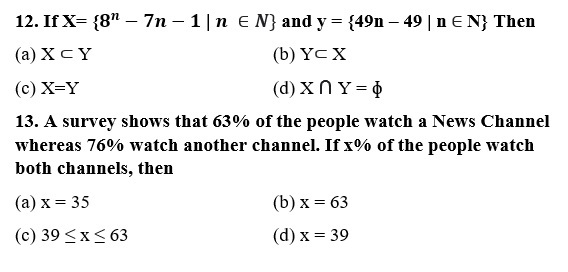
14. In a statistical investigation of 1003 families of Calcutta, it was found that 63 families has neither a radio nor a T.V. 794 families has a radio and 187 has T.V. the number of families in that group having both a radio and a T.V. is
(a) 36 (b) 41
(c) 32 (d) None of these
15. If sets A and B are defined as
A = {(x, y) | y = 1/x, x ≠ 0, x ∈ R},
B = {(x, y) | y = – x, x ∈ R,}. Then
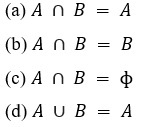
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
16. If A = {1, 3, 5, 7, 9, 11, 13, 15, 17}, B = {2, 4,…, 18} and N the set of natural number is the universal set, then (A’ ∪ (A ∪ B) ∩ B’) is
(a) ɸ (b) N
(c) A (d) B
17. If S = {x | x is a positive multiple of 3 less 100} and P = {x | x is a prime number less than 20}. Then n(S) + n(P) is equal to
(a) 34 (b) 31
(c) 33 (d) 41
18. If X and Y are two sets and X’ denotes the complement of X, then X ∩ (X ∪ Y)’ is equal to
(a) X (b) Y
(c) ɸ (d) X ∩ Y
19. Let n(U) = 700, n(A) = 200, n(B) = 300 and n(A ∩ B) = 100, then n(Ac ∩ Bc )=
(a) 400 (b) 600
(c) 300 (d) 200
20. If A and B are two sets, then A ∪ B = A ∩ B iff
(a) A ⊆ B (b) B ⊆ A
(c) A = B (d) None of these
21. If aN = {ax : x ∈ N}, then the set 3N ∩ 7N is
(a) 21 N (b) 10 N
(c) 4N (d) None of these
22. Given n (U) = 20, n(A) = 12, n(B) = 9, n(A ∩ B) = 4, where U is the universal set, A and B are subsets of U, then n
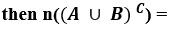
(a) 17 (b) 9
(c) 11 (d) 3
(e) 16
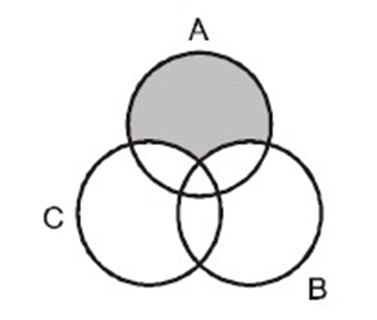
23. The shaded region in the given figure is
(a) A ∩ (B ∪ C)
(b) A ∪ (B ∩ C)
(c) A ∩ (B – C)
(d) A – (B ∪ C)
24. A set contains 2n +1 elements. The number of subsets of this set containing more than n elements is equal to

25. If A and B are two sets then (A-B)U(B-A)U(A∩B) is equal to
(a) A ∪ B (b) A ∩ B
(c) A (d) B’
26. Consider the following relations :
(1) A – B = A – (A ∩ B)
(2) A = (A ∩ B) ∪ (A – B)
(3) A – (B ∪ C) = (A – B) ∪ (A – C)
Which of these is/are correct?
(a) 1 and 3
(b) 2 only
(c) 2 and 3
(d) 1 and 2
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
27. Let A and B be two sets then (A ∪ B)’ ∪ (A’ ∩ B) is equal to
(a) A’ (b) A
(c) B’ (d) None of these
28. Let U be the universal set and A ∪ B ∪ C = U . Then {(A – B) ∪ (B – C) ∪ (C – A)}’ is equal to
(a) A ∪ B ∪ C (b) A ∪ (B ∩ C)
(c) A ∩ B ∩ C (d) A ∩ (B ∪ C)
29. If A, B and C are three sets such that A ∩ B = A ∩ C and
A ∪ B =A ∪ C , then
(a) A = C (b) B = C
(c) A ∩ B = ɸ (d) A = B
30. Let X= {1, 2, 3, 4, 5} . The number of different ordered pairs (Y, Z) that can be formed such that Y ⊆ X, Z ⊆ X and Y ∩ Z is empty, is

31. Let A and B be two sets containing 2 elements and 4 elements respectively. The number of subsets of AB having 3 or more elements is
(a) 256 (b) 220 (c) 219 (d) 211
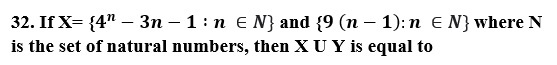
(a) N (b) Y – X (c) X (d) Y
33. In a certain town, 25% of the families own a phone and 15% own a car, 65% families own neither a phone nor a car and 2000 families own both a phone and a car. Consider the following three statements:
(1) 5% families own both a phone and a car
(2) 35% families own either a phone or a car
(3) 40,000 families live in the town
Then
(a) one (1) and (2) are correct
(b) one (1) and (3) are correct
(c) ones (2) and (3) are correct
(d) all (1), (2) and (3) are correct
34. Let S = {1,2,3,… ,….,100}. The number of non-empty subsets A of S such that the product of elements in even is
35. In a class of 140 students numbered 1 to 140, all even numbered students opted mathematics course, those whose number is divisible by 3 opted Physics course and those whose number is divisible by 5 opted Chemistry course. Then the number of students who did not opt for any of the three courses is
(a) 102 (b) 42
(c) 1 (d) 38
ANSWER KEYS
| 1. (c) | 11. (b) | 21. (a) | 31. (c) |
| 2. (c) | 12. (a) | 22. (d) | 32. (d) |
| 3. (d) | 13. (c) | 23. (d) | 33. (d) |
| 4. (c) | 14. (b) | 24. (d) | 34. (a) |
| 5. (c) | 15. (c) | 25. (a) | 35. (d) |
| 6. (b) | 16. (b) | 26. (d) | |
| 7. (b) | 17. (d) | 27. (a) | |
| 8. (d) | 18. (c) | 28. (c) | |
| 9. (c) | 19. (c) | 29. (b) | |
| 10. (d) | 20. (c) | 30. (d) |
ALSO VISIT : WORK , POWER AND ENERGY JEE QUESTIONS
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SETS QUESTIONS FOR JEE MAINS
