DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
Table of Contents
STATISTICS CLASS 10 ICSE
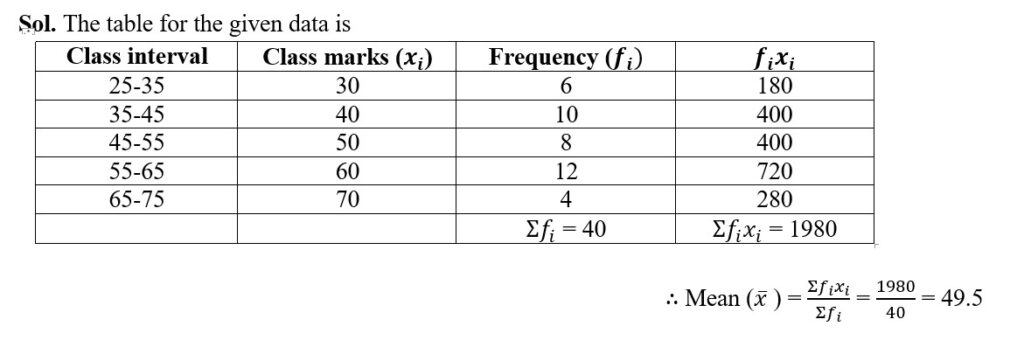
1. Find the mean of the following data by direct method.
| Class interval | 25-35 | 35-45 | 45-55 | 55-65 | 65-75 |
| Frequency | 6 | 10 | 8 | 12 | 4 |
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
2. Find the median of the first ten prime numbers.
Sol. First ten prime numbers in ascending order are 2, 3, 5, 7, 11, 13, 17, 19, 23 and 29.
Here, n = 10 (even)
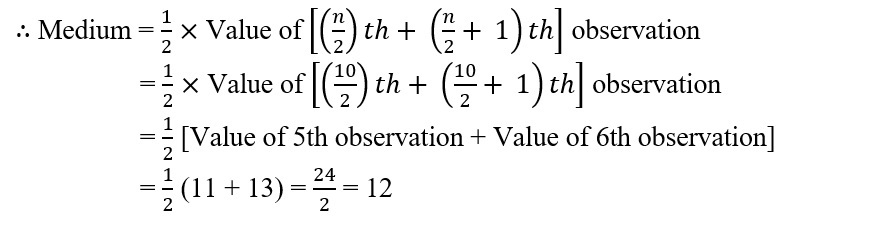
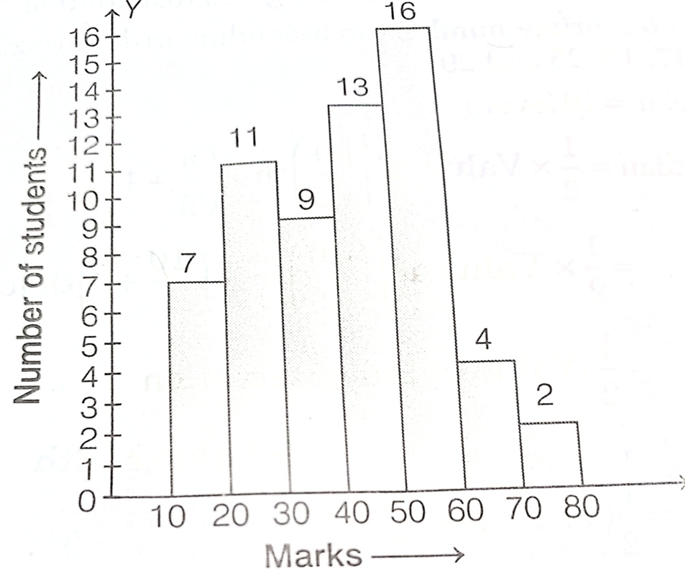
3. Represent the following frequency distribution by means of a histogram.
| Marks | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Number of students | 7 | 11 | 9 | 13 | 16 | 4 | 2 |
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
Sol. We represent the class intervals along the X-axis on a suitable scale and the corresponding frequencies along the Y-axis on a suitable scale. We construct rectangles with class intervals as bases and the corresponding frequencies as heights. Thus, we obtain a histogram as shown below.
4. Find the mean of the following distribution by step-deviation method.
| Class interval | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency | 10 | 6 | 8 | 12 | 5 | 9 |
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
Sol. Here, class width, h = 30 – 20 = 10.
The table for the given data is

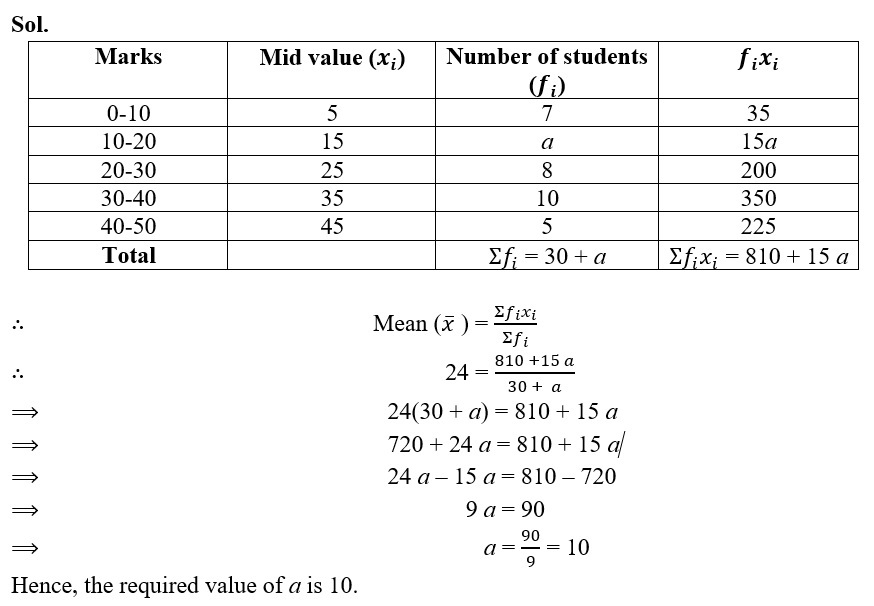
5. If the mean of the following distribution is 24, find the value of ‘a’.
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Numbers of students | 7 | a | 8 | 10 | 5 |
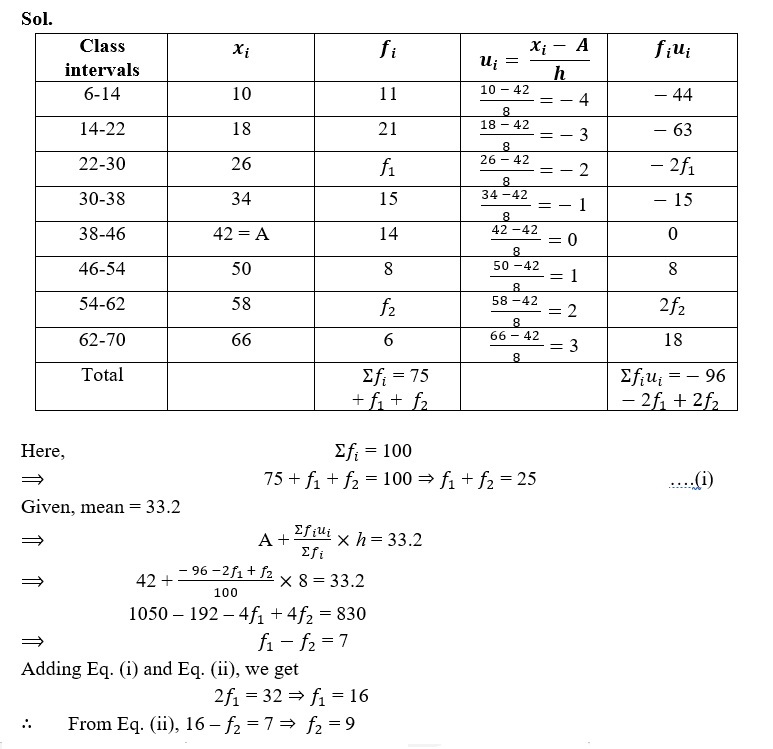
6. If the mean of the distribution is 32.2 and the sum of all frequencies is 100, then find the missing frequencies f 1 and f 2.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
| Class | 6-14 | 14-22 | 22-30 | 30-38 | 38-46 | 46-54 | 54-62 | 62-70 |
| Frequency | 11 | 21 | f 1 | 15 | 14 | 8 | f 2 | 6 |
7. 200 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in English alphabets in the surnames was obtained as follows
| Number of letters | 0-5 | 5-10 | 10-15 | 15-20 | 20-25 |
| Number of surnames | 20 | 60 | 80 | 32 | 8 |
Find the median of the above data.
Sol. The cumulative frequency table of given data is

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
8. Find the missing frequencies in the following frequency distribution table, if n = 100 and median is 32.
| Marks obtained | Number of students |
| 0-10 | 10 |
| 10-20 | ? |
| 20-30 | 25 |
| 30-40 | 30 |
| 40-50 | ? |
| 50-60 | 10 |
| Total | 100 |

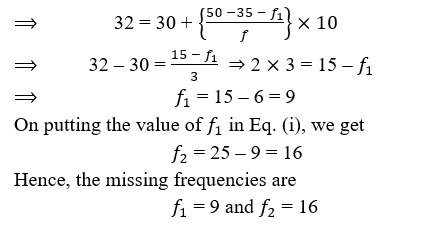
9. The weight of 50 workers is given below
| Weight (in kg) | Number of workers |
| 50-60 | 4 |
| 60-70 | 7 |
| 70-80 | 11 |
| 80-90 | 14 |
| 90-100 | 6 |
| 100-110 | 5 |
| 110-120 | 3 |
Sol. The cumulative frequency table for the continuous distribution is shown below
| Weight (in kg) | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 |
| Frequency ( f ) | 4 | 7 | 11 | 14 | 6 | 5 | 3 |
| Cumulative frequency (cf) | 4 | 11 | 22 | 36 | 42 | 47 | 50 |
On the graph paper, we plot the following points A(60, 4), B(70, 11), C(80, 22),
D(90, 36), E(100, 42), F(110, 47) and G(120, 50), join all these points by a free hand drawing.
The required ogive is shown on the graph paper given below.

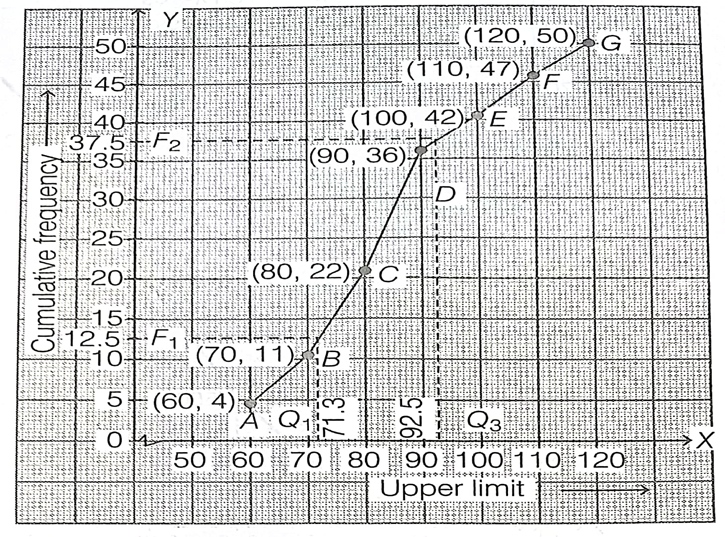
(ii) On the ogive, the point (95, y) corresponds to y = 40.
So, cf id 40. Therefore, the number of variates above 95 kg is 50 – 40 = 10
10. The daily wages of 80 workers in a project are given below.
| Wages | Numbers of workers |
| 400-450 | 2 |
| 450-500 | 6 |
| 500-550 | 12 |
| 550-600 | 18 |
| 600-650 | 24 |
| 650-700 | 13 |
| 700-750 | 5 |
Sol. Let us first prepare the following cumulative frequency table
| Wages ( in ₹) | Number of workers | Cumulative frequency |
| 400-450 | 2 | 2 |
| 450-500 | 6 | 8 |
| 500-550 | 12 | 20 |
| 550-600 | 18 | 38 |
| 600-650 | 24 | 62 |
| 650-700 | 13 | 75 |
| 700-750 | 5 | 80 |
In order to draw an ogive for the given distribution, we assume a class 350-400 before the first class interval with zero frequency.
Now, we mark the upper class limits (including the imagined class) along X-axis and the cumulative frequency along Y-axis on the following scale.
2 cm = ₹50 on X-axis, 2 cm = 10 workers on Y-axis
On the scale, we plot the points (400, 0), (450, 2), (500, 8), (550, 20), (600, 38),
(650, 62), (700, 75) and (750, 80) with the help of following graph.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: STATISTICS CLASS 10 ICSE
ALSO VISIT:
10th ICSE
