DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
Introduction to Quadratic Polynomials and Quadratic Equations
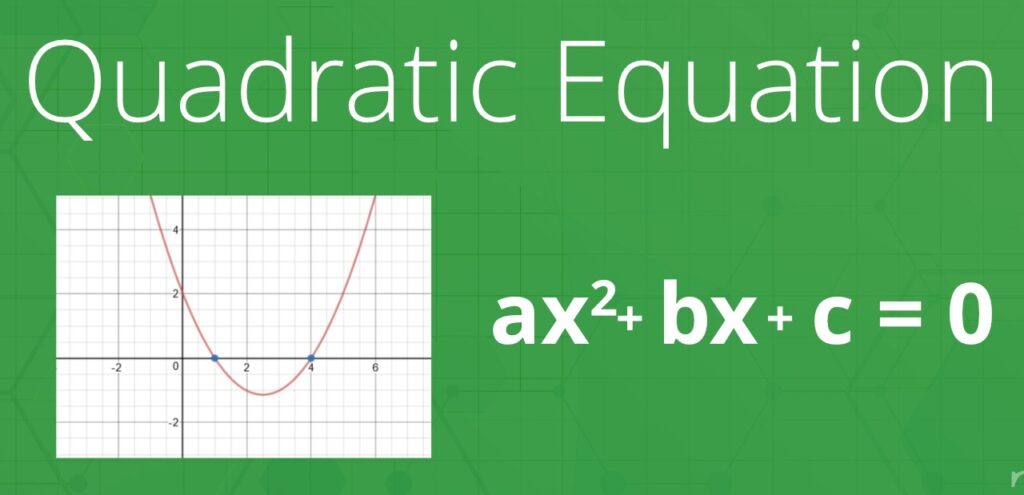
Quadratic polynomial: A polynomial of degree two is known as quadratic polynomial. p(x) = ax2 + bx + c is a quadratic polynomial where a 0 and a, b, c are real numbers.
Quadratic equation: If p(x) is a quadratic polynomial then p(x) = 0 is known as a quadratic equation, i.e. ax2 + b x + c = 0 as known as a quadratic equation. Here a 0 and a, b, c are real numbers. e.g. 2x2 7x + 5 = 0 is quadratic equation. Here a = coefficient of x2 = 2 ; b = coefficient of x = 7 c = term independent of x = 5
Solution of a Quadratic Equation by Factorisation
To find the solution of a quadratic equation by factorisation, we first write the given quadratic equation as product of two linear factors by splitting the middle term. By equating each factor to zero we get possible solutions/roots of the given quadratic equation.
For Example: Find the roots of the equation x2 5x + 6 = 0 by factorization.
Solution of Quadratic Equation Using Quadratic Formula or Discriminate Method
Let quadratic equation be ax2 + bx + = 0
Step 1. Find D = b2 4ac.
Step 2. (i) If D > 0, solution/roots of the quadratic equation are given by
x =
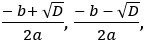
(ii) If D = 0, solution/roots of the quadratic equation are given by x = .
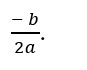
(iii) If D < 0, equation has no real roots.
Tips
If question is “State whether the following equation represents a quadratic equation
2x(x 3) + 4 = x(2x + 1) + 5?”
Then, solution is given as
“2x(x 3) + 4 = 2x2 + x + 5
2x 6x + 4 = 2x2 + x + 5
7x + 1 = 0
The given equation is not of the form ax2 + bx + c = 0
Hence, it is not a quadratic equation.”
Note: But don’t solve as “2x(x 3) + 4 = x(2x + 1) + 5 is not of the form ax2 + bx + c = 0
Hence, this is not a quadratic equation.”
Here, students are advised not to answer orally which is not preferred.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
Table of Contents
QUADRATIC EQUATIONS CLASS 10
1. Which of the following is not a quadratic equation?
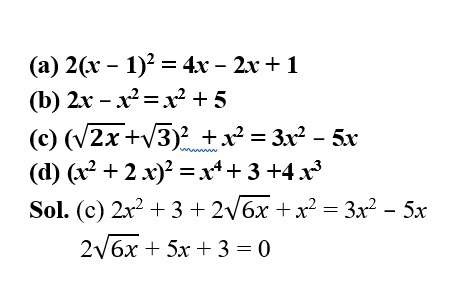
2. If x = 3 is one root of the quadratic equation x2 2kx 6 = 0, then find the value of k.
Sol. Putting x = 3 in x2 2kx 6 = 0, we get
32 2k 3 6 = 0
9 6k 6 = 0
3 6k = 0
3 = 6k
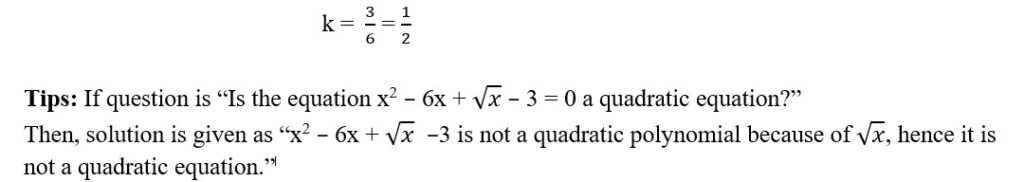
Note: But don’t solve as “yes, it is a quadratic equation, as degree of equation is 2” This is a wrong statement.
3. Find the roots of the following quadratic equations by factorization:
(i) x2 3x – 10 = 0
(ii) 2x2 + x – 6 = 0
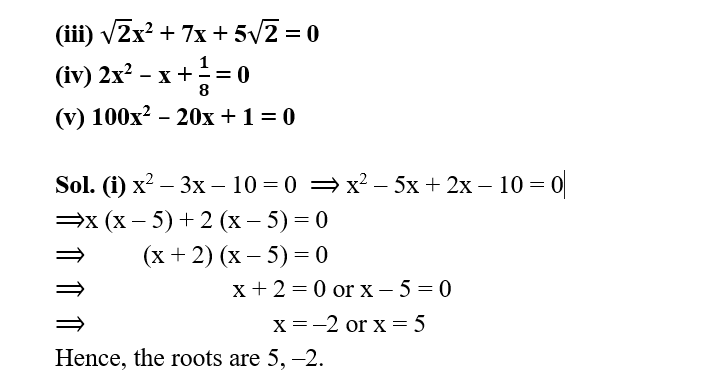
(ii) 2x2 + x – 6 = 0
2x2 + 4x – 3x – 6 = 0
2x(x + 2) – 3 (x + 2) = 0
(2x – 3) (x + 2) = 0
2x – 3 = 0 or x + 2 = 0
2x = 3 or x = – 2
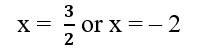

(v) 100x2 – 20x + 1 = 0
100x2 – 10x – 10x + 1 = 0
10x (10x – 1) – 1(10 – 1) = 0
(10x – 1) (10x – 1) = 0
10x – 1 = 0 or 10x – 1 = 0
4. Find two consecutive positive integers, sum of whose squares is 365.
Sol. Let the two consecutive integers be x and x + 1
ATQ x2 + (x + 1)2 = 365
x2 + x2 + 2x + 1 = 365
2x2 + 2x – 364 = 0
x2 + x – 182 = 0
x2 + 14x – 13x – 182 = 0
x(x +14) – 13(x + 14) = 0
(x – 13) (x + 14) = 0
x = 13, – 14 (– 14 is rejected because it is a negative integer)
Hence, the two consecutive positive integers are 13 and 13 + 1 = 14.
5. Solve the following quadratic equation by factorisation:
12abx2 – (9a2 – 8b2) x – 6ab = 0
Sol. 12abx2 – (9a2 – 8b2) x – 6ab = 0
12abx2 – 9a2x + 8b2x – 6ab = 0
3ax (4bx – 3a) + 2b (4bx – 3a) = 0
4bx – 3a) (3ax + 2b) = 0
4bx – 3a = 0 or 3ax + 2b = 0
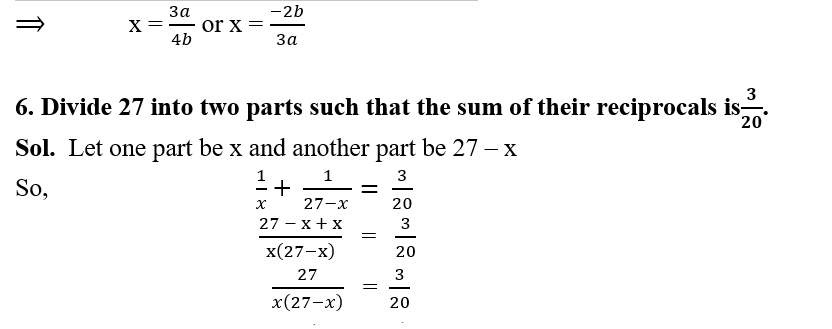
180 = x (27 – x)
x2 – 27x + 180 = 0
(x – 15) (x – 12) = 0
x = 15, x = 12
so, two parts are 15 and 12
Tips
If question is “solve for x, 4x2 – 2(a2 + b2) x + a2b2 = 0.”
Then, solve as
“4x2 – 2a2x – 2b2x + a2b2 = 0
2x (2x – a2) – b2 (2x – a2) = 0
(2x – b2) (2x – a2) and then proceed further.”
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
This is important to notice that in these questions as far as possible we should try by splitting the middle term (i.e. term with x) and factorisation.
Note: but don’t solve as
“D = [– 2(a2 + b2)] – 4 4 a2b2
= 4(a2 + b2) – 16 a2b2 and proceed further
This is a lengthy method, finding the discrimination and applying the formula, which sometimes can be lengthy calculations.
7. Solve for x : 9x2 – 9(a + b)x + (2a2 + 5ab + 2b2) = 0.
Sol. 9x2 – 9(a + b) x + (2a2 + 5ab + 2b2) = 0
Here, A = 9, B = 9(a + b), C = 2a2 + 5ab + 2b2
D = B2 – 4AC
= [– 9(a + b)] 2 – 4 9(2a2 + 5ab + 2b2)
= 81(a + b) – 36(2a2 + 5ab + 2b2)
= 81(a2 + b2 + 2ab) – 72a2 – 180ab – 72b2
= 9a2 + 9b2 – 2ab) = 9(a – b)2
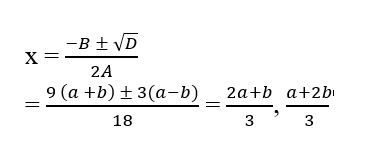
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
8. Speed of a boat in still water is 15 km/h. It goes 30km upstream and returns back at the same point in 4 hours 30minutes. Find the speed of the stream.
Sol. Speed of boat in still water = 15km/h
Speed of the stream be x km/h
Speed of the boat for downstream = (15 + x) km/h
And the speed of the boat for upstream = (15 – x) km/h
Distance = 30km

x = –5 is rejected because speed of stream cannot be negative
x = 5km/h
Hence, speed of the stream is 5km/h
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
9. Find two consecutive odd natural numbers, the sum of whose squares is 394.
Sol. Let first odd natural number be (2x – 1)
And other consecutive odd natural number is (2x + 1)
So,
(2x – 1)2 + (2x + 1)2 = 394
4x2 + 1 – 4x + 4x2 + 1 + 4x = 394
8x2 + 2 = 394
8x2 = 394
x2 = 49
x = 7
First odd natural number = (2 x 7 – 1) = 13
Next odd natural number = (2 x 7 + 1) = 15
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
10. A train travels at a certain average speed for a distance of 63 km and then travels at a distance of 72 km at an average speed of 6 km/hr more than its original speed. If it takes 3 hours to complete total journey, what is the original average speed?
Sol. Let original average speed of the train be x km/h
New average speed be (x + 6) km/h

3(x2 + 6x) = 135x + 378
= 3(45x + 126)
x2 + 6x = 45x + 126 = 0
x2 – 39x – 126 = 0
x2 – 42x + 3x – 126 = 0
x(x – 42) + 3(x – 42) = 0
(x – 42) (x + 3) = 0
x – 42 = 0 or x + 3 = 0
x = 42 or x = –3 (rejected)
Therefore, original average speed of the train is 42 km/h.
11. Solve the following for x:
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
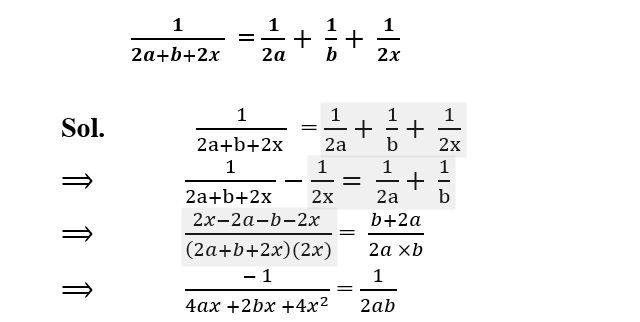
4x2 + 2bx + 4ax = 2ab
4x2 + 2abx + 4ax + 2ab = 0
2x (2x + b) + 2a(2x + b) = 0
(2x + b) (2x + 2a) = 0
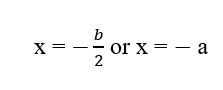
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
NATURE OF THE ROOTS OF QUADRATIC EQUATION AND APPLICATION OF QUADRATIC EQUATIONS
• Let given quadratic equations is a2 + bx + c = 0. a 0
Here D = b2 4ac
(i) If D > 0, then quadratic equation has two unequal real roots.
(ii) If D=0, then quadratic equation has two equal real roots.
(iii) If D < 0, then quadratic equation has no real roots.
• If are roots of the quadratic equation
ax2 + bx + c = 0, a 0
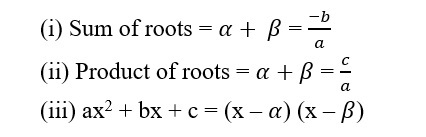
• If are roots of a quadratic equation then quadratic equation is given by x²
(sum of the roots) x + product of the roots = 0

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
• Let given quadratic equation is ax2 + bx + c = 0, a 0
(i) If a, b and c are rational and D, 1.e.b2 – 4ac is a perfect square then roots of the quadratic equation are rational.
(ii) If a, b and c are rational and D, i.e. b2 – 4ac > 0 and D is not a perfect square then both the roots of the quadratic

13. Which of the following equations has no real roots?
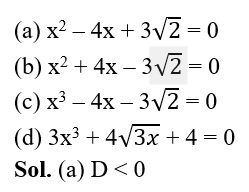
14. (x2 + 1) – x2 = 0 has
(a) Four real roots
(b) Two real roots
(c) No real roots
(d) One real root
Sol. (c) no real roots
15. Find the value of k for which the equation x2 + k(2x + k – 1) = 0 has real and equal roots.
Sol. x2 + k(2x + k – 1) = 0
x2 + 2kx + k2 – k = 0
Here, a = 1, b = 2k, c = k2 – k
Since, the roots are real and equal
D = b2 – 4ac = 0
(2k)2 – 4 1 (k2 – k) = 0
4k2 – 4k2 + 4k = 0
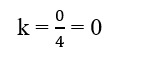
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
16. Find the value of p so that the quadratic equation px(x – 3) + 9 = 0 has two equal roots.
Sol. px(x – 3) + 9 = 0
px2 – 3px + 9 = 0
Here, a = p, b = – 3p, c = 9
For equal roots D = 0
D = b2 – 4ac
(– 3p)2 – 4 p 9 = 0
9p2 – 36p = 0
9p(p – 4) = 0
9p = 0 or p – 4 = 0
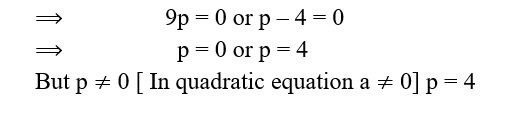
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
17. Find the value of K for which the roots of the quadratic equation
(k – 4) x2 + 2(k – 4) x + 2 = 0 are equal
Sol. Given equation is (k – 4) x2 + 2(k – 4) x + 2 = 0
Here a = k – 4, b = 2 (k – 4), c = 2
D = b2 – 4ac
= [2(k – 4)]2 – 4 (k – 4) 2
= 4 (k – 4)2 – 8(k – 4)
For equal roots, D = 0
4(k – 4)2 – 8(k – 4) = 0
4(k – 4) [(k – 4) – 2] = 0
k = 4 or k = 6

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
18. If the equation (l + m2)x2 + 2mcx + c2 – a2 = 0 has equal roots, then show that c2 = a2 (l + m2)
Sol. The given equation is
( l + m2)x2 + 2mcx + c2 – a2 = 0
Here A = (l + m2), B = 2mc, C = c2 – a2
This equation has equal roots
D = 0
B2 – 4AC = 0
(2mc)2 – 4 (l + m2)(c2 – a2) = 0
4m2c2 – 4(c2 – a2 + m2c2 – m2a2) = 0
4m2c2 – 4c2 + 4a2 – 4m2c2 + 4m2a2 = 0
–4c2 + 4a2 + 4m2a2 = 0
4c2 – 4a2 – 4m2a2 = 0
c2 – a2 – m2a2 = 0
c2 = a2 + m2a2
c2 = a2(l + m2)
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
19.Show that if the roots of the following quadratic equation are equal then ad = bc
x2 (a2 + b2) + 2(ac + bd)x + (c2 + d2) = 0
Sol. Given equation is
x2 (a2 + b2) + 2(ac + bd)x + (c2 + d2) = 0
Roots are equal, B2 – 4AC = 0
[2(ac + bd)]2 – 4[a2 + b2] [c2 + d2] = 0
4a2c2 + 4b2d2 + 8acbd – 4a2c2
– 4a2d2– 4b2c2 – 4b2d2 = 0
8acbd– 4a2d2– 4b2c2 = 0
4(ad – bc)2 = 0
ad – bc = 0
ad = bc
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
ALSO VISIT :
10TH CBSE
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRATIC EQUATIONS CLASS 10
