DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9
This article is on chapter constructions for class 9 students and contains ncert questions with detailed explanations and answers. students can get constructions class 9 solutions by reading this article
CONSTRUCTIONS
Geometrical Construction: It is the process of drawing a geometrical figure using only two instruments- a ruler and a compass. Although, protractor may be used for drawing non-standard angles.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9
BASIC CONSTRUCTIONS
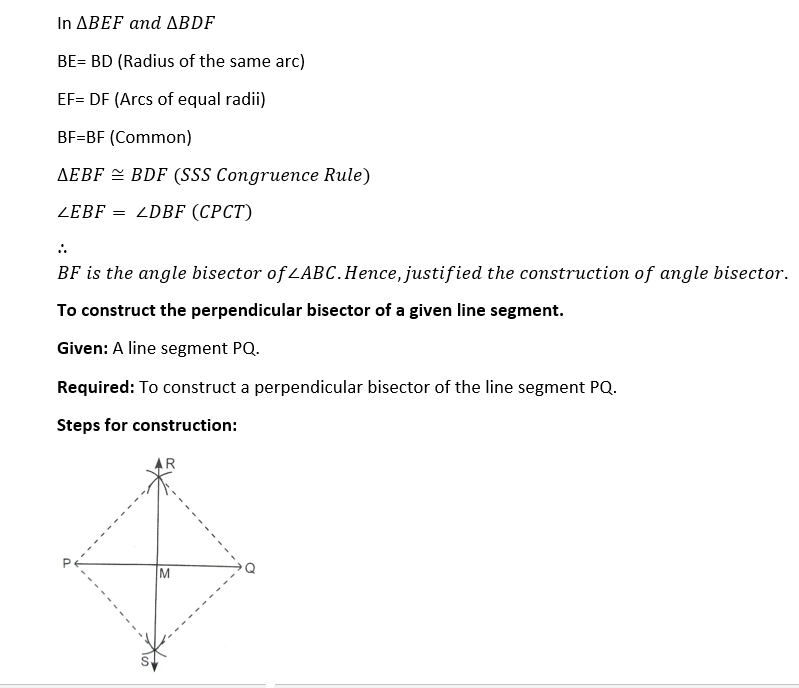
To construct the bisector of given angle.
Given: An Angle ABC.
Required: To construct the bisector of ∠ABC
Steps of construction:
(i)Draw any acute angle ABC. With B as center and of any radius, draw an arc DE to intersect BA at D and BC at E.
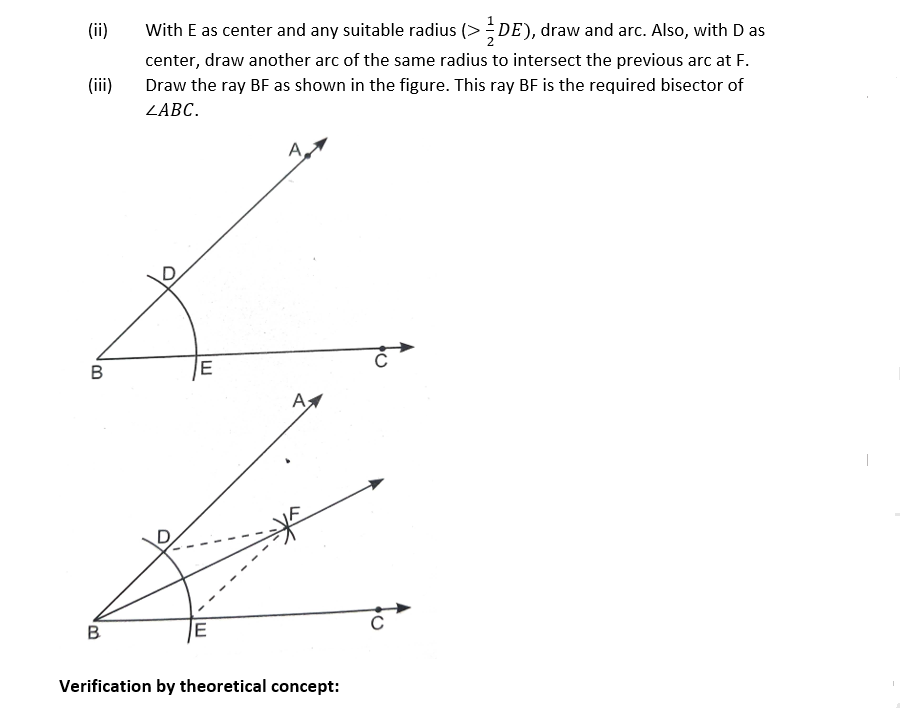
Join DF and EF.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9


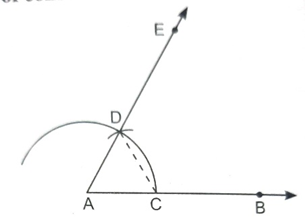
(i) Take a ray AB with initial point A.
(ii) Taking A as centre and with a suitable radius, draw an arc which intersects AB, say at a point C.
(i) Taking C as centre and with the same radius as in step (ii), draw an arc, intersecting the previously drawn arc, say at a point D.
(ii) Draw the ray AE passing through D. Then, ∠EAB is the required angle of 60°.
Justification:
Join CD.
Then, AC=CD = DA (By construction)
Therefore, ∠ACD is an equilateral triangle and we know that each angle of an equilateral triangle is 60°.
∠DAC=60° or ∠EAB = 60°
Hence, our construction for an angle of 60° is justified.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9
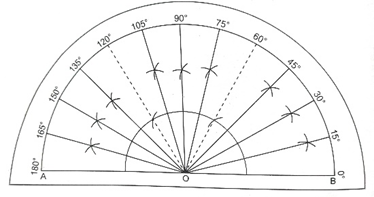
Angle Bisectors: The following figure shows the constructions of various angles which are multiples of 15 in the anti-clockwise direction drawn with the help of a ruler and a compass.
CONSTRUCTION OF A TRIANGLE
A triangle is unique if:
(i) Two sides and the included angle is given.
(ii) Three sides are given
(iii) Two angles and included side is given
(iv) In a right triangle, hypotenuse and one side is given
If above combination(s) are not given, then we have to find the way to construct the triangle uniquely.
For example: To Construct a triangle,
(i) Given its base, a base angle and
(a) Sum of other two sides
(b) The difference of the other two sides.
(ii) Given its parameter and its two base angles.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9
Table of Contents
CONSTRUCTIONS CLASS 9 NCERT SOLUTIONS
1. With the help of a ruler and a compass it is not possible to construct an angle of:
(a) 37.5°
(b) 40° `
(c) 22.5°
(d) 67.5°

2. The construction of a triangle ABC in which AB = 45° is not possible when difference off BC and AC is equal to
(a) 3.5cm
(b) 4.5 cm
(c) 3 cm
(d) 2.5 cm
Sol. when BC – AC = 4.5 cm, so BC – AC > AB i.e. BC > AC +AB, which is not possible
Correct option is (b)
3. Is it possible to construct the angle of 37.5° with the help of ruler and compass?
Sol. Yes, it is possible by constructing 75° angle and bisecting it, we can obtain 37.5° angle.
4. Do you agree with the statement ‘ XYZ can be constructed, if Y = 90° , Z = 75° and XY +YZ + ZX = 11.5 cm’.
Sol. Yes, because two base angles and perimeter is given and Y + Z = 90° + 75° = 165° ∠180°
5. Can you construct a ABC, if AB = 6.5 cm A = 60 and BC +AC = 11 cm.
Sol. Yes, with given dimensions, we can construct the ABC because BC + AC > AB.
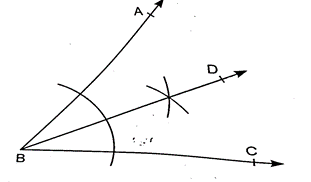
6. Using protractor, draw an angle of 53° into equal parts by bisecting it as shown in the figure.
Sol. Yes, we can divide ABC = 52° into two equal parts by bisecting it as shown in the figure
7. Construct a triangle whose sides are in the ratio 1:3:5 and whose perimeter is 18cm.
Sol. Given ratio of sides of a triangle = 1 : 3 : 5
Let the length of sides of a triangle be x, 3x and 5x respectively
Perimeter of triangle =18 cm
x + 3x + 5x = 18
9x = 18
x = 2 cm
Sides of triangle are 2 cm, 6 cm and 10 cm.
Here, we find that 2 cm + 6 cm < 10 cm.
So, construction of given triangle would not be possible
8. Draw an angle of an equilateral triangle, using protractor. Bisect it using compass.
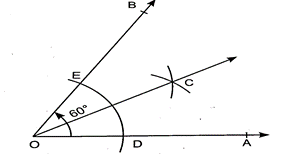
Each angle of an equilateral triangle is 60°
According to question, ∠AOB = 60°
OC is the bisector of ∠AOB.
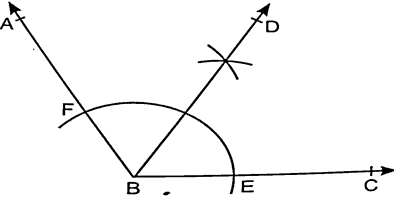
9. Draw obtuse angle. Bisect it using compass.
Sol. Let ∠ABC = 120°
Draw the bisector BD of ∠ABC as shown in the figure
10. Construct an equilateral triangle, given its one side is 5 cm
Sol. We know that all sides of an equilateral triangle are equal
In ABC, AB = BC = CA = 5 cm.
Steps of construction
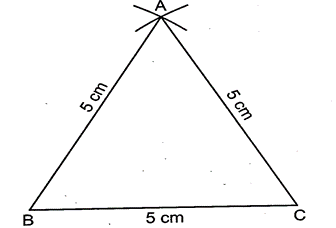
(i) Draw a line segment, BC = 5 cm
(ii) Taking B and C as centres and radius equal to 5 cm, draw arcs which interest each other at A.
(iii) Join AB and AC.
Thus,
ABC is the required equilateral triangle.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9
11. Construct a triangle ABC in which BC = 5 cm, ∠B = 75° and AB + AC = 9 cm.
Sol. Steps of construction:

(i) Draw a line segment BC = 5 cm. At point B, construct an ∠XBC = 75°
(ii) Cut a line segment BD = AB + AC = 9 cm from the ray BX.
(iii) Join CD
(iv) Draw the Perpendicular bisector PQ of CD which interest BD at A.
(v) Join AC.
(vi) Then, ABC is the required triangle. This is because point A lies on the perpendicular bisector of CD
AD = AC
BD = AB + AD = AB + AC
12. Draw a line segment PQ = 8.4 cm. Divide it into four equal parts using a ruler and a compass.
Sol. Steps of construction
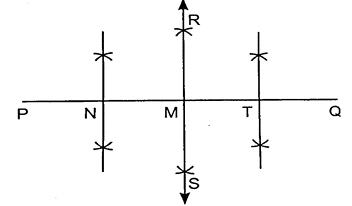
(i) Draw a line segment PQ = 8.4 cm.
(ii) Taking P and Q as centres and radius more than 1/2 PQ, draw arcs above and below the line segment PQ interesting at R and S respectively as shown.
(iii) Join RS. Let it interest PQ at M. The ray RS divides the line segment PQ into two equal parts PM and QM.
(iv) In a similar way, draw perpendicular bisectors of PM and QM which divides Each PM and QM into two equal parts again as shown.
So, the four equal parts of line segment PQ are PN = NM = MT = TQ. On measuring them, they all are equal to 2.1 cm.
13. Construct a triangle ABC in which BC = 5.8 cm, ∠B = 45° and ∠C = 60° . Construct angle bisector of ∠B and ∠C and interest them at point O. Measure ∠BOC.
Sol. Steps of construction:
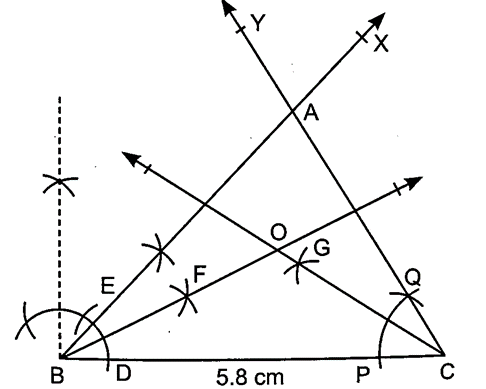
(i) Draw a line segment BC = 5.8 cm
(ii) At B and C, draw
∠XBC = 45 and ∠YCB = 60°
(iii) The rays XB and YC intersect at A. Therefore, ∠ABC is the required triangle.
(iv)Taking D and E as centres with radius greater than 1/2 DE, draw arcs intersecting each other at F.
(vi) Draw the ray BF. It is the angle bisector of ∠B.
(vii) Similarly, construct angle bisector CG of ∠C.
(viii) Let BF and CG interest each other at O.
(ix) On measuring ∠BOC, we get BOC = 127°
14. Draw any acute angle. Divide it into four equal parts using a ruler and a compass. Measure them using protractor.
Sol. Steps of construction:
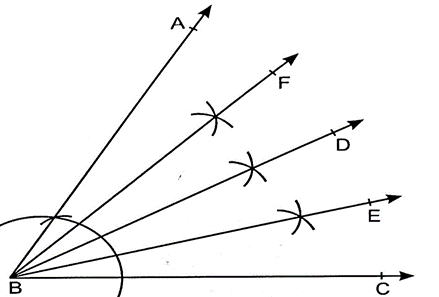

ALSO VISIT : 1.quadrilaterals class 9
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CONSTRUCTIONS CLASS 9
