DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS
This post is on the topic of surface areas and volumes class 9 CBSE . this post is ideal to learn surface areas and volumes class 9 formulas , surface area and volume class 9 questions answers and students can also get surface area and volume class 9 solutions of their questions or problems on this topic .
SURFACE AREAS AND VOLUMES
1. Cuboid: Outer surface of a cuboid is made up of six rectangles called the faces of the cuboid.
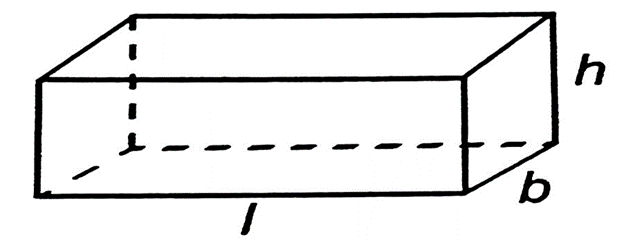
Diagonal of cuboid =
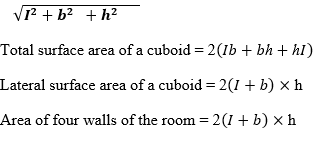
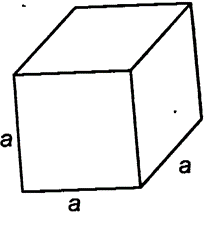
2. Cube: Cuboid, whose length, breadth and height are all equal, is called a cube

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS
Table of Contents
SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS
1. The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of 10 per m² is 15000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area]
Sol. Let length of floor of rectangular hall = l
Let breadth of floor of rectangular hall = b
Perimeter of floor of rectangular hall= 2(l + b)
2(l+b) = 250 m
Let height of the room be h.
Area of four walls of the room= 2(l+b) h = 250 m² [From (i)]
Given cost of painting the four walls per m² = Rs.10
Total cost of painting the four walls of Rs.250 m²
=₹250x10xh
According to question
= 250 10 h = Rs. 15000
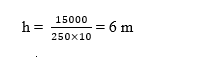
Height of the hall = 6 m
2. The paint in a certain container is sufficient to paint an area equal to 9.375 m². How many bricks of dimensions 22.5 cm 10 cm 7.5 cm can be painted out of this container?
Sol. Given dimensions of a brick are
l = 22.5 cm, b = 10 cm, h = 7.5 cm
Total surface area of a brick
= 2(lb + bh + hl)
= 2(22.5 10 + 10 7.5 + 7.5 22.5)
= 2(225 +75 + 168.75) = 2 468.75
= 937.5 cm² = 0.09375 m²
The paint in a container is sufficient to paint an area
= 9.375 m²
and Area of one brick = 0.09375 m²
Total number of bricks which can be painted
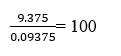
3. A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
Sol. (i) Given dimensions of herbarium are l = 30 cm, b = 25 cm, h = 25 cm
Total surface area of herbarium (including top and base)
= 2(lb + bh + hl)
= 2(30
25 + 25 25 + 25 30)
= 2(750 + 625 + 750)
= 2 2125 = 4250 cm²
(ii) Total tape needed for all 12 edges
= 4(l + b + h)
= 4(30 + 25 + 25)
= 4 x 80 = 320 cm
4. How do we judge that the given object is a solid object?
(a) By touching it.
(b) By finding its dimensions.
(c) Distance between any two points of the object remains same.
(d) By keeping it on the table and noting down whether the whole object touches the table or not.
Sol. d) By keeping it on the table and noting down whether the whole object touches the table or not.
5. Number of surfaces of the same area in a cuboid are
(a) 6
(b) 4
(c) 2
(d) 3
Sol. (c) we have one pair of opposite faces which have same areas
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS
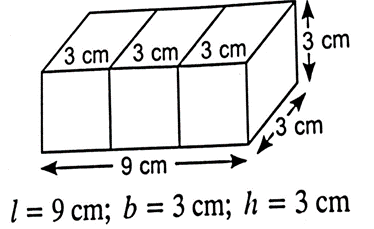
6. Three cubes are joined end to end forming a cuboid. If side of a cube is 3 cm, then dimensions of the cuboid are:
(a) l = 2, b = 2, h = 2
(b) l = 4, b = 4, h = 2
(c) l = 4, b = 2, h = 4
(d) 1=9, b = 3, h = 3
Sol. (d) New dimensions are:
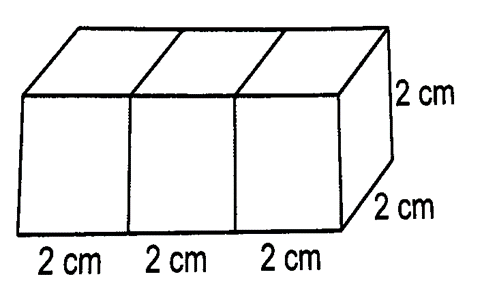
7. Three cubes are joined end to end forming a cuboid. If side of a cube is 2 cm, find the dimensions of cuboid thus obtained.
Sol. Given side of cube is 2 cm. Three cubes are joined end to end.
Dimensions of cuboid thus formed are (2 + 2 + 2) cm, 2 cm, 2 cm, i.e. 6 cm, 2 cm, 2 cm.

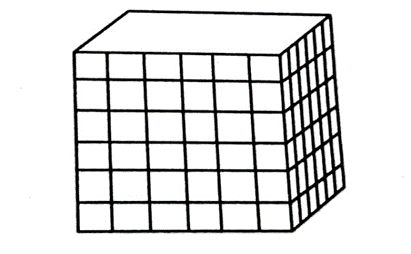
9. Three equal cubes are placed adjacent to each other in a row. Find the ratio of the total surface area of the cuboid thus formed to the total surface area of the three cubes.
Sol. Let edge of three equal cubes be a
Surface area of one cube = 6a²
Total surface area of three cubes = 3 x 6a² = 18a2
Three equal cubes are joined end to end, a cuboid is formed as shown.
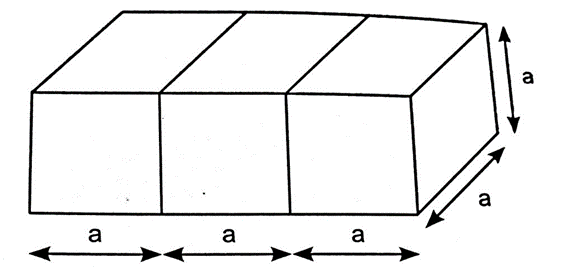
Length of resulting cuboid = 3a
Breadth of resulting cuboid = a
Height of resulting cuboid = a


DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS


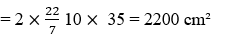
15. Circumference of the base of a cylinder open at the top is 132 cm. The sum of radius and height of the cylinder is 41 cm. Find the cost of polishing the outer surface of cylinder at the rate of 10 per square metre.
Sol. Let radius of cylinder be r cm.



1. Curved surface area of a cone = πrl
2. Area of circular base of a cone = πr²
Area of base ring = (R²-r²)
R = External radius; r = Internal radius
3. Total surface area of a cone = πr(r +l)
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS
17. Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Sol. Given diameter of base of cone = 10.5 cm


ALSO VISIT : 1.quadrilaterals class 9
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: SURFACE AREAS AND VOLUMES CLASS 9 SOLUTIONS
