Table of Contents
CIRCLES CLASS 9 QUESTIONS FOR CBSE STUDENTS
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CIRCLES CLASS 9 QUESTIONS

11. Sector is the region between the chord and its corresponding arc.
Ans. False
Sector is the region between the arc and the two radii of the circle.
12. A circle is a plane figure.
Ans. True
A circle can be drawn of the surface. Hence, it is called a plane figure.
13. Given a circle of radius r and with centre O. A point P lies in Plane such that OP r. Then point P lies
(a) In the interior of the circle
(b) On the circle
(c) In the exterior of the circle
(d) Cannot say
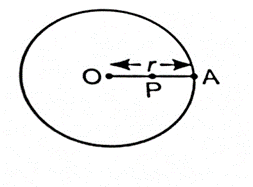
Sol. Let a point A lies on the circle as shown in the figure.
Then OA = r and OP< r
⟹ OP < OA
This shows that point P lies in the interior of the circle.
Correct option is (a)
14. Given a circle with centre O and chords AB, PQ and XY. Point P, Q and O are collinear and radius of a circle is 6 cm. Then mark the correct option.
(a) AB = XY = 3cm
(b) AB = 6cm = XY
(c) PQ = 6cm
(d) PQ = 12cm
Sol. Since points P, O and Q are collinear and O is centre of a circle, so PQ is a diameter of a circle.
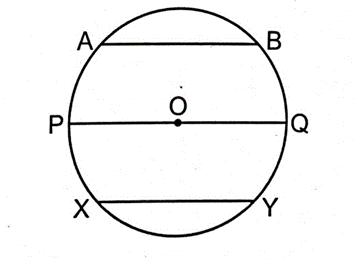
⟹ PQ = 2
radius
⟹ PQ = 2 6 = 12 cm
Correct option is (d)
15. Given a circle with centre O and smallest chord AB is of length 3cm, longest chord CD is of length 10cm and chord PQ is length 7cm, then radius of the circle is
(a) 1.5cm
(b) 6cm
(c) 5cm
(d) 3.5cm
Sol. (c)
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CIRCLES CLASS 9 QUESTIONS
16.The region between an arc and the two radii, joining the centre to the end points of the arc is called a/an
(a) Sector
(b) Segment
(c) Semicircle
(d) Arc
Sol. (a)
17. In how many parts a plane can divide a circle if it interest perpendicularly?
(a) 2 parts
(b) 3 parts
(c) 4 parts
(d) 8 parts
Sol. (a)
18. Through three collinear points, a circle can be drawn.
(a) True
(b) False
Sol. (b)
Because a circle through two points cannot pass through a point which is collinear to these two points.
19. A, B and C are three points on a circle. Prove that perpendicular bisectors of AB, BC and CA are concurrent.
Sol. Given: A, B and C are three points on the circle.
To prove: Perpendicular bisector of AB, BC and CA are concurrent.
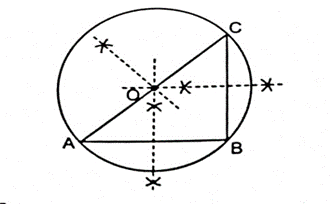
Proof:
(i) Draw the perpendicular bisectors of AB
(ii) Draw perpendicular bisector of BC. Both the perpendicular bisectors interest at a point ‘O’. This point ‘O’ is called the centre of the circle.
(iii) Now, draw perpendicular bisector of AC. We observe that perpendicular bisector of AC also passes through the same point O.
Hence, all the three perpendicular bisector are concurrent, i.e. they pass through the same point.
Reason: Three or more lines passing through the same point are called concurrent lines.
20. Two congruent circles with centres O and O′ interest at two points A and B. Then
AOB = AO′B. Write True or False, and justify your answer.
Sol. Two circles with centres O and O’ are congruent. AB is the common chord.
Then AOB = AO’B (true)
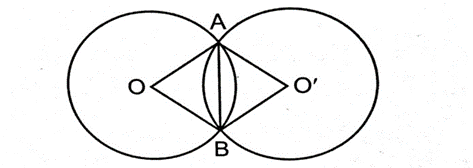
Construction: Join OA, OB, O’A and O’B
Justification: In
AOB and AO’B
OA = O′A (Radii of congruent circles)
OB = O′B (Radii of congruent circles)
AB = AB (common)
AOB AO’B (By SSS congruence rule)
AOB = AO’B (By CPCT)
Hence proved. Therefore, it is true
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: CIRCLES CLASS 9 QUESTIONS
