Table of Contents
POLYNOMIALS CLASS 9 CBSE -MATHEMATICS
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: POLYNOMIALS CLASS 9


Sol. (d)
12. Zeros of the polynomial p (x) = (x – 2)² – (x + 2)² are
(a) 2, – 2
(b) 2x
(c) 0, – 2
(d) 0
Sol. p(x) = (x – 2)² – (x + 2)² = x² +4 – 4x- (x² + 4 + 4x)
= x2 + 4 – 4x – x² – 4 – 4x
= -8x
Now, p(x) = 0
-8x = 0
x = 0
Correct option is (d).
13. Which of the following expressions are polynomials in one variable and which are not? Which are not polynomials in one variable? State reasons for your answer.
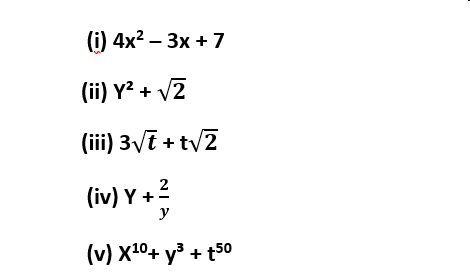
(i) The expression is a polynomial with one variable.
(ii) The expression is a polynomial in one variable.
(iii) The given algebraic expression is not a polynomial because the exponent of the variable in the given polynomial is not a whole number.
(iv) The given algebraic expression is not a polynomial because the exponent of the variable in the given polynomial is not a whole number.
(v) This expression is a polynomial in three variables.
14. Write the coefficients of x2 in each of the following
(i) 2 + x2 + x
(ii) 2 – x2 + x3
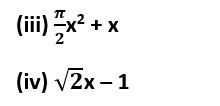
Sol. Coefficients of x2 in each expression are
(i) 1
(ii) – 1
(iii)
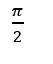
(iv) 0
15. Write the coefficients of r2 in each of the following:
(i) ax2 + bx + c
(ii) 4x2 + 5x – 3
(iii) 3 – 5x2 + x3
(iv)
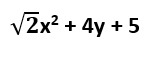
Sol. The coefficients of x2 in each of the given polynomials are:
(i) a
(ii) 4
(iii) – 5

Sol. The coefficients of x3 in the given expressions are:
(i) 5

17. Write the degree of each of the following polynomials:
(i) 4x5 – 3x4 + 9
(ii) 3 – 2y2 + 5y3 – 2y8
(iii) 3
(iv) 4y + 5
Sol. The highest power of the variable in a polynomial is called the degree of the polynomial. Hence, degree of the given expressions is
(i) 5
(ii) 8
(iii) 0 ( 3 = 3x )
(iv) 1
18. Write the coefficient of y in the expansion of (5 – y)2.
Sol. (5 – y) = 52 – 2 x 5 x y = y2
[Using (a – b)2 = a2 – 2ab + b2]
= 25 – 10y + y2
Required coefficient of y = – 10
19.What is the value of the polynomial x2 + 8x + k, if – 1 is a zero of the polynomials?
Sol. p(x) = x² + 8x + k
If – 1 is a zero of the polynomial p(x), then
p(-1) = 0 → (-1)² + 8(-1) + k = 0
1-8 + k = 0 → k = 7

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: POLYNOMIALS CLASS 9
21. If f(x) = 5x² – 4x + 5, find f(1) + f(- 1) + f(0)
Sol.
f(x) = 5x² – 4x + 5
f(1) = 5(1)² – 4(1) + 5 = 5 – 4 + 5 = 6
f(-1) = 5(-1)² -4(- 1) + 5 = 5 + 4 + 5 = 14
f (0) = 5(0)² – 4.0 + 5 = 0 – 0 + 5 = 5
f(1) + f(-1) + f(0) = 6 + 14 + 5 = 25
22. Let R1 and R2 are the remainders when polynomial f(x) = 4x3 + 3x² + 12ax – 5 and g(x) = 2x³ + ax² – 6x – 2 are divided by (x – 1) and (x – 2) respectively. If 3R1 + R2 – 28 = 0, find the value of a.
Sol. Given: f(x) = 4x3 + 3x2 + 12ax – 5 and
g(x) = 2x3 + ax2 – 6x – 2
Now, R1 = remainder when f(x) is divided by x – 1
R1 = f(1)
R1 = 4(1)3 + 3(1)2 +12a(+1) – 5
= 4 + 3 + 12a – 5 = 12a + 2
And, R2 = remainder when g(x) is divided by x – 2
R2 = g(2)
= 2(2)3 + a (2)2 – 6 (2) – 2
= 16 + 4a – 12 – 2 = 4a + 2
Substituting the values of R1 and R2 in 3R1 + R2 – 28= 0, we get
3(12a + 2) + 4a + 2 – 28 = 0
36a + 6 + 4a – 26 = 0
40a = 20
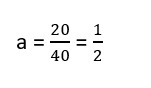
23. State Factor Theorem. Using this theorem, factorize x3-3x2 -x + 3.
Sol. Factoring Theorem: If p(x) is a polynomial of degree n
1 and a is any real number, then
(i) x = a is a factor of p(x), if p(a) = 0 and
(ii) p(a) = 0 If (x – a) is a factor of p(x)
Let p(x) =x³ – 3x² -x + 3 ..(i)
Factor of 3 are ± 1, and ±3.
By trial method,
p(1) = 13 – 3(1)2 – 1 + 3
= 1-3-1+ 3 = 0
Therefore, by the factor theorem, (x – 1) is a factor of p(x).
Similarly, p(-1) = (-1)³ – 3(-1)² -(-1) + 3
= -1-3 + 1 + 3 = 0
So, (x +1) is also a factor of p(x) and p(3) = (3)³ – 3(3)2 – 3 + 3 = 27 – 27 – 3 + 3 = 0
So, (x – 3) is also a factor of p(x).
Since p(x) is a polynomial of degree 3, so it cannot have more than three linear factors.
Let p(x) = k(x – 1) (x + 1)(x – 3) …(ii)
x3 – 3x2 – x + 3 = k(x – 1)(x + 1) ( x – 3)
Putting x = 0 both the sides x = 0, we get
3 = k(-1)(1)(-3) = 3k
k = 1
Putting k = 1 in equation (ii) we get
f(x) = (x – 1)(x + 1)(x – 3) DOWNLOAD MOBILE APPLICATION TO LEARN MORE: POLYNOMIALS CLASS 9 24. If 2x + 3y = 12 and xy = 6, then find the value of 8x3 + 27y3.
Sol. we know that (x + y)3 = x3 + y3 + 3xy(x +y)
x3 + y3 = (x + y)³ – 3xy(x + y)
Now, 8x3 + 27y3 = (2x)³ + (3y)³
= (2r + 3y)³ – 3(2x)( 3y)(2x + 3y)
= 123 – 18 × 6 x 12 [Given 2x + 3y = 12 and xy = 6]
= 1728 – 1296 = 432
Hence, 8x3 + 27y3 = 432
ALSO VISIT : GRAVITATION CLASS 9
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: POLYNOMIALS CLASS 9
