DOWNLOAD MOBILE APPLICATION TO LEARN MORE: PROBABILITY CLASS 9

DOWNLOAD MOBILE APPLICATION TO LEARN MORE: PROBABILITY CLASS 9
This post contains probability class 9 mcq , probability class 9 questions with solutions this is the ideal post on probability for class 9 students and contains extra questions for probability class 9. probability class 9 solutions are provided in this post .
PROBABILITY
EXPERIMENT (ACTION OR OPERATION)
Some important objects for experiment
- Trial
- Coin
- Die or dice
- Cards (52)
- Balls, Boys, etc.
P(E)= (Number of trials in which the event (E) has happened/ Total number of trials)
- 0 ≤ P(E) ≤ 1
- Probability of occurrence of an event + Probability of non-occurrence of that event = 1
- Sum of all probabilities = 1 or P(E₁) + P(E₂) + P(E3) + … P(E) = 1
Number of Experiments:
(i) When a coin is tossed,
P(getting a head),
P(H)= (Number of heads/ Total number of trials)
and P(getting): tail),
P(T) = (Number of tails/ Total number of trials)
Also,
P(H) + P(T) = 1
(ii) When a die is tossed,
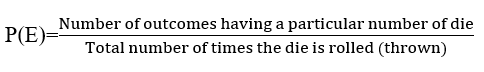
and P(E1) + P(E2) + P(E3) + P(E4) + P(E5) + P(E6) = 1
Where
P(E1) = Probability of an event of getting outcome 1.
P(E2) = Probability of an events of getting outcome 2 and so on.
Note: In the similar way, one can find the probability of other experiments.
Probability of an event can be any fraction from 0 to 1.
P(E) + P (not E) = 1
• The empirical (or experimental) probability depends on the number of trials undertaken and the number of times the outcomes occurs in these trials.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: PROBABILITY CLASS 9
Table of Contents
PROBABILITY CLASS 9 QUESTIONS WITH SOLUTIONS
1. In a cricket match, a batswoman hits a boundary 6 times out of 30 balls she plays. Find the probability that she did not hit a boundary.
Sol. Number of times that a batswoman hits a boundary = 6.
Total number of balls she played = 30
Number of times that she did not hit a boundary= 30 – 6 = 24
Probability of batswoman does not hit a boundary,

2. Three coins are tossed simultaneously 200 times with the following frequencies of different outcomes:
Outcome
| Outcome | 3 heads | 2 heads | 1 head | No head |
| Frequency | 23 | 72 | 77 | 28 |
If the three coins are simultaneously tossed again, compute the probability of 2 heads coming up.
Sol. Total number of outcomes = 200
Number of times 2 heads coming up = 72
P(2 heads will come up)

3. Probability of an event can be
(a) – 0.7
(b) 11/9
(c) 1.001
(d) 0.6
Sol. (d) Probability of an event lies between 0 and 1 (both inclusive).
4. The probability of happening of an event is 45%. The probability of an event is
(a) 45
(b) 4.5
(c) 0.45
(d) 0.045
Sol. (c), 45% means 45 out of 100. Therefore, probability = 45/100 = 0.45
5. In a class of 40 students, there are 110% girls. Then the number of girls is
(a) 44
(b) 22
(c) 30
(d) None of these
Sol. (d) Maximum is 100%. So, 110% is not valid.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: PROBABILITY CLASS 9
6. Which of the following words represent uncertainty?
(a) Probability
(b) Value
(c) Event
(d) None of these
Sol. (a) probability
7. Probability represents
(a) Uncertainty
(b) Certainty
(c) Numerical measure of uncertainty
(d) Numerical measure of certainty.
Sol. (c) Numerical measure of uncertainty
8. In an experiment, probability of an event is better approximated, when an experiment is performed
(a) 10 times
(b) 20 times
(c) 30 times
(d) Large number of times
Sol. (d) large number of times
9. Empirical probability of an event is also known as
(a) An experimental probability
(b) A theoretical probability
(c) Theoretical expectation of a chance
Sol. (a) an experimental probability
10. An experiment is performed and probability of an event A is recorded, probability of an event A can be
(a) 0.001
(b) 1.999
(c) 1.001
(d) – 0.999
Sol. (a) 0.001, because 0 P (E) 1
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: PROBABILITY CLASS 9
11. An experiment is performed 350 times and there are three possible events A, B and C in an experiment. Possible occurrences of three events are recorded, which records are possible?
(a) A : 166, B : 80, C : 94
(b) A : 90, B : 0, C : 250
(c) A : 200, B : 100, C : 50
(d) A : 110, B : 110 C : 110
Sol. (c) Here A = 200 , B = 100 , C = 50
As possible occurrence of three events are shown,
Total possible outcomes
=A + B + C = 200 + 100 + 50 = 350
These are equal to number of trials,


15. Write the sample space of a coin tossed three times.
Sol. S(E)= {HHH, TTT, HHT, HTH, THH, TTH, THT,HTT}
:. Total number of sample space = 8
16. A card is drawn at random from a well shuffled pack of 52 cards. Find the probability that the card drawn is a red card.
Sol. Total number of red cards in a well shuffled pack of 52 cards = 26
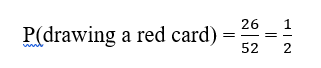
17. 1000 families with 2 children were surveyed, and the following data were recorded:
| Number of girls in a family | 0 | 1 | 2 |
| Number of families | 111 | 614 | 275 |
If a family is chosen at random, compute the probability that it has:
(i) Exactly 1 girl
(ii) Exactly 2 girls
Sol. Total number of families = 1000
(i) Number of families that have exactly 1 girl= 614
P(a family that has exactly one girl)

18. If the probability of winning a game is 0.4, what is the probability of losing it?
Sol. We know that P(E) + P(not E) = 1
i.e. P(winning a game) + P(losing a game) = 1
→ P (losing a game) = 1 – P(winning a game)
= 1 – 0.4 = 0.6
Hence, probability of losing the game = 0.6
19. A bag contains 12 balls out of which x balls are white. If one ball is taken out from the bag, find the probability of getting a white ball. If 6 more white balls are added to the bag and the probability now for getting a white ball is double the previous one, find the value of x.
Sol. Total number of balls = 12
Number of white balls = x

20. A purse contains a number of ₹ 1, ₹ 2 and ₹ 5 coins as given below: ₹ 1, ₹ 2 and ₹ 5 coins as given below:
| ₹ 1 | ₹ 2 | ₹ 5 |
| 10 | 14 | 14 |
If from the purse a coin is taken out at random, then find the probability that the coin
(i) is not a ₹ 1 coin
(ii) is a ₹ 3 coin
Sol. Total number of coins =10 + 14 + 14 = 38
(i) Total number of 1 coin = 10

21. The daily cost of milk (in ₹) supplied to 25 houses in a locality are given below:
| Cost (in ₹) | Number of horses |
| 40 – 50 | 4 |
| 50 – 60 | 5 |
| 60 – 70 | 3 |
| 70 – 80 | 5 |
| 80 – 90 | 2 |
| 90 – 100 | 6 |
If one house is chosen at random, find the probability that
(i) The milk bill of the house lies between ₹ 60 and ₹ 80.
(ii) House is paying at most ₹ 69, for the milk bill.
(iii) The milk bill of the house is below ₹ 50.
Sol. Total number of houses = 25
(i) Total number of houses paying the milk bill between ₹60 and ₹80 = 3 + 5 = 8

22. A parent has collected data of number of schools based on the monthly fees, so that he can choose the school for admission of his child. The data is as follows:
| Monthly fees of schools (in ₹) | Number of schools |
| 250 – 500 | 14 |
| 500 – 750 | 16 |
| 750 – 1000 | 18 |
| 1000 – 1250 | 12 |
| 1250 – 1500 | 14 |
| 1500 – 1750 | 8 |
| 1750 – 2000 | 8 |
If a school is selected at random, find the probability that the school is having
(i) Minimum fee.
(ii) Maximum fee.
(iii) Fee less than ₹ 1000.
(iv) Fee ₹ 1000 or more but less than ₹ 1500.
Sol. Total number of schools
=14 + 16 + 18 + 12 + 14 + 8 + 8 = 90
(i) Number of schools having minimum fee (in the range ₹ 250 – ₹ 500) = 14

23. The given table shows the marks obtained by 50 students out of 100 in history examination.
| Marks obtained | Number of students |
| 0 – 25 | 9 |
| 25 – 50 | 8 |
| 50 – 75 | 23 |
| 75 – 100 | 10 |
| Total | 50 |
A student is chosen at random.
(i) Find the probability that he has obtained 75 or more marks.
(ii) If 50% are passing marks, find the probability of the students failing in history examination.
(iii) Find the probability that the student has obtained less than 75 marks.
Sol. Total number of students = 50
(i) Number of students who has obtained 75 or more marks = 10
P(a student has obtained 75 or more marks)

24. Two coins are tossed 729 times and the outcomes are recorded below:
| Outcomes | Frequency |
| No tail | 189 |
| One tail | 297 |
| Two tail | 243 |
Find the probability of each event. Also, find the probability that at least one tail will come.


Sol. (b)
27. In a medical examination of students of a class, the following blood groups are recorded:
| Blood group | A | AB | B | 0 |
| Number of students | 10 | 13 | 12 | 5 |
A student is selected at random from the class. The probability that he/she has blood group B, is

28. Two coins are tossed 1000 times and the outcomes are recorded as below:
| Number of heads | 2 | 1 | 0 |
| Frequency | 200 | 550 | 250 |
Based on this information, the probability for at most one head is

(d) 9/16
Sol. (d)
ALSO VISIT : 1.quadrilaterals class 9
5. SURFACE AEAS AND VOLUMES CLASS 9
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: PROBABILITY CLASS 9
