DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRILATERALS CLASS 9

Quadrilaterals for class 9 is an important topic this article contains the important points to remember and different types of quadrilaterals along with their properties . this post contains quadrilaterals 9 notes , quadrilaterals class ncert solutions , quadrilaterals class 9 mcq.
QUADRILATERALS
Definition: A quadrilateral is a simple closed figure with four sides, four angles and four vertices.
Types of Quadrilaterals: There are five types of quadrilaterals:
- Parallelogram
- Rectangle
- Square
- Rhombus
- Trapezium
Kite is also a special type of quadrilateral.
Angle sum property of a Quadrilateral: One common property of all quadrilaterals is that the sum of all their angles equals to 360 .
PROPERTIES OF DIFFERENT QUADRILATERALS
All sides are congruent
Opposite sides are parallel and congruent
All angles are congruent
Opposite angles are congruent
Diagonals are congruent
Diagonals are perpendicular
Diagonals Bisect each other
Adjacent angles are supplementary.
PROPERTIES OF PARALLELOGRAM
Opposite sides are parallel and congruent
Opposite angles are congruent
Diagonals Bisect each other
Adjacent angles are supplementary.
PROPERTIES OF RECTANGLE
Opposite sides are parallel and congruent
All angles are congruent
Opposite angles are congruent
Diagonals are congruent
Diagonals Bisect each other
Adjacent angles are supplementary.
PROPERTIES OF RHOMBUS
All sides are congruent
Opposite sides are parallel and congruent
Opposite angles are congruent
Diagonals are perpendicular
Diagonals Bisect each other
Adjacent angles are supplementary.
PROPERTIES OF SQUARE
All sides are congruent
Opposite sides are parallel and congruent
All angles are congruent
Opposite angles are congruent
Diagonals are congruent
Diagonals are perpendicular
Diagonals Bisect each other
Adjacent angles are supplementary.
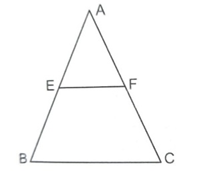
THE MID-POINT THEOREM
THE MID-POINT THEOREM
The line segment joining the mid-points of two sides of a triangle is parallel to the third side.

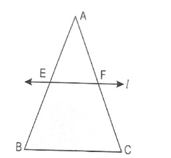
Converse of Mid-point theorem
The line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRILATERALS CLASS 9
Table of Contents
QUADRILATERALS CLASS 9 CBSE MATHEMATICS
(a) 90°
(b) 75°
(c) 65°
(d) 10°
Ans. C

(a) A parallelogram
(b) A square
(c) A rhombus
(d) A rectangle
Ans. B
3. Given a quadrilateral ABCD, and diagonals AC and BD bisect each other at P such that AP = CP and BP = DP. Also APD = 90°, then quadrilateral is a
(a) Rhombus
(b) Trapezium
(c) Parallelogram
(d) Rectangle
Ans. A
4. Given a rectangle ABCD and P, Q, R, S are the mid-points of AB, BC, CD and DA respectively. Length of diagonals of a rectangle is 8 cm. Then the quadrilateral PQRS is a
(a) Parallelogram with adjacent sides 4 cm and 6 cm
(b) Rectangle with adjacent sides 4 cm and 6 cm
(c) Rhombus with side 4 cm
(d) Square with side 4 cm.
Ans. C
5. Can the angles 110 , 80 , 70 and 95 be the angles of a parallelogram? Why or why not?
Ans. No
6. Can all the angles of a quadrilateral be right angles? Give reason for your answer.
Ans. Yes
7. In the given figure, BX and CY are perpendiculars to a line through the vertex A of ABC and Z is the mid – point of BC. Prove that XZ = YZ.
Sol. Given: BX and CY are Perpendiculars to a line XAY.
To prove: XZ = YZ
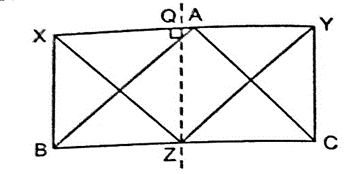
Construction:
8. ABCD is a trapezium in which AB || DC. M and N are the mid-points of AD and BC respectively. If AB = 12 cm and MN = 14 cm, find CD.
Sol. Here, ABCD is a trapezium in which, AB|| DC and M and N arethe mid-points of AD andBC respectively.
Since the line segment joining the mid-points of non-parallel sides of a trapezium is half of the sum of the lengths of its parallel sides,
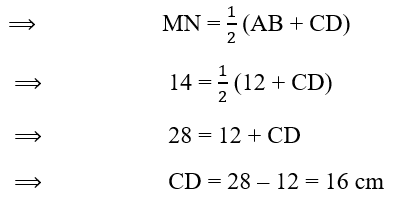
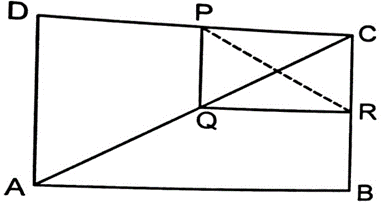
9. In the given figure, ABCD and PQRC are rectangles and Q is the mid-point of AC. Prove that:
(i) DP = PC
(ii) PR = AC

Sol. Given: ABCD and PQRC are two rectangles and Q is the mid-point of AC.
To prove: (i) DP = PC
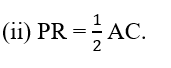


DOWNLOAD MOBILE APPLICATION TO LEARN MORE: QUADRILATERALS CLASS 9
